Formal Systems: An Overview
David Hilbert laid many of the foundations for what are now known as formal systems. His formalist program aimed to develop axioms that would yield the desired truths of math and geometry, without reliance on intuition. These axioms would be true regardless of whether they were interpreted in terms of points, lines, planes, or in terms of "
law, love, and chimney sweeps".
Formal systems allow mathematical results to be described and assessed with increased precision, and are particularly useful with theories that deal with more than three dimensions.
In a formal system, the whole process of proof is reduced to the manipulation of symbols according to rules that complicitly determine the conclusions that can be drawn from a set of axioms. Intuitions about the "meaning" of the symbols play no role in the workings of the formal system. Such meanings are only introduced with the interpretation of the system.
Below is an example of a simple formal system designed for application to the logic of truth. Note that in addition to the standard interpretation in terms of truth, there are also other interpretations that satisfy the formal system (for more explanation see "The Lowenheim-Skolem Theorem" Map 3 Box 107).
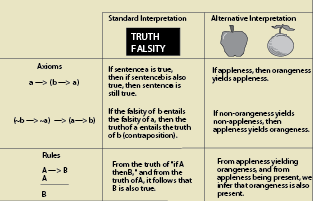
This formal system is not complete with respect to the logic of truth; that is it does not yield all valid formulas of the logic of truth. But recall that it does not even make sense to ask whether the system iteslf is complete or correct; the system in itself is just an orderly set of patterns of symbols with rules to govern their recombination.
For more on formal systems, see Map 4 and the "
Can functional states generate consciousness?" argument on Map 6.
The Steps of Gödel's Proof1) The
Principia Mathematica gave Gödel a way to translate natural language statements into a formal system of proof. With this formal system in hand, Gödel was able to prove that all such systems strong enough to produce arithmetic are inherently limited. Illustration of the proof begins with an English version of what will become the notorious Gödel sentence: "G says it is not provable that G."
2) In step two, the sentence is roughly translated into the formal system of
Principia Mathematica. The formalisation shown here is not well formed (i.e. it is not grammatically correct), and consequently the system of proof used in
Principia Mathematica cannot be applied to it. To make the sentence truly self-referential and well formed we must first develop a way to make well formed sentences that refer to themselves.
3) To that end, each symbol in the formal system is replaced with a code number.
4) Those numbers are then used as exponents in a series of prime numbers that will be multiplied together into one large Gödel number. This step ensures that every Gödel number corresponds to one and only one formula in the formal system of
Principia Mathematica.
5) This number is then represented symbolically in this case by a long string of S's followed by zero (where the number of S'sis equal to the Gödel number). The symbolic numeral representation is necessary that the Gödel number can be dealt with formally in the
Principia Mathematica.
6) This numeral representation for Gödel numbers allows us to use
Principia Mathematica to "talk about itself". In particular, we can plug the Gödel numeral for G back into the formula itself. This genrates a well-formed Gödel sentence that makes reference to itself, and that can be assessed using the proof system of
Principia Mathematica.
7) Now we are in a position to show that the Gödel sentence is neither provable or disprovable using the system of
Principia Mathematica. To see how the paradox works see "Self-referential paradoxes" on this map.
8) However, the Gödel sentence can be recognised to be a true from outside of the system. This is the aspect of the proof that later interpreters would focus on in the context of machine intelligence.
Various authors, notably John Lucas and Roger Penrose, extended Gödelian insight to computers. They pointed out that because computers are a kind of formal system, the same limitations discovered by Gödel in
Principia Mathematica and other formal systems might apply to computers as well.
Note: A variety of simplifications have been used in order to illustrate in a readable way the general idea behind Gödel's extremely complex proof:
- Gödel does not begin with a non-well formed formula and then fix it as we've done—this is just rhetorically useful way to present the proof.
- The Gödel sentence does not make reference to itself in the simple ways suggested by the its informal versions. The numeral for G—and the sentence G itself—correspond precisely in that there is a one-to-one coding between them, but they do not have the same “meaning.” They are “extensionally equivalent” but not “intensionally equivalent.”