http://blogs.cornell.edu/info2040/2012/11/10/understanding-ibms-watson/ Fundamental in all the various applications of Watson is his ability to do natural language question-answering. Answering questions posed in natural language may seem like a trivial task to many people, and this is indeed so – we pose and answer questions in natural language every day with relative ease, so much so that we take for granted the great complexities that natural language poses to computers. While computer programs are natively explicit and exacting in their calculations over symbols and numbers, they falter when working with natural language. This is because natural language is implicit, highly contextual, ambiguous and often imprecise. What is most notable is that Watson, in all its intricacies, ultimately relies on the deceivingly simple concept of Bayes’ Rule in negotiating the semantic complexities of natural language.
To illustrate this, consider an example of a question posed in the form of a Jeopardy! clue:
Category: Self-contradictory words
It’s to put to death legally, or to start, as in a computer program.
Answer: Execute
For Watson to properly answer that question, he has to first decompose the question by parsing the sentence into words from which he attempts to derive meaning from. Effectively, when given words and phrases like “self-contradictory”, “put to death legally”, “start” and “computer program”, Watson has to infer semantically from these words and deduce the right answer.
Watson may for instance shortlist words like “kill”, “start”, “begin” and “execute” as possible answer candidates, with only the last candidate being the correct answer. However, Watson also considers the context given by the other words and phrases in the question in determining the most probable answer. This inference is essentially done using Bayes’ Rule.
For example, Watson could be considering the answer candidate “execute” as the answer to return. In doing this, Watson considers the following probabilities:
P(R) = P(“execute” is relevant) – probability of the word “execute” being relevant
P(“put to death” occurs) – the probability of the phrase “execute” occurring
P(“computer program” occurs) – the probability of the phrase “computer program” occurring
.. and so on for other words and phrases.
Using Bayes’ Rule, Watson is able to derive the probability of P(R | some word occurs) given that P(some word occurs | R). The latter probability comes from the huge repository of documents that Watson has processed. These documents give Watson the various probabilities of different words occurring given that “execute” is a relevant word in a document. Using Bayes’ Rule, Watson can determine the probability that the word “execute” is relevant in a context in which the phrase “computer program” occurs.
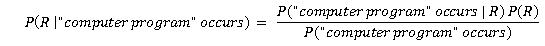
Watson essentially does this for all the key words and phrases in the question, and derives the most probable answer by calculating the various conditional probabilities. Naturally, among all the probable answer candidates, “execute” would be the most relevant (and hence the most likely answer) given that it occurs most frequently alongside other words like “computer program” and “put to death”.
While this illustration admittedly trivialises the complexity of the semantic understanding that Watson is capable of, it still sheds light on the fundamental importance of Bayes’ Rule, as a mathematical concept, in laying the grounds for such complicated inference tools.