Fisher's linear discriminant[edit]
The terms Fisher's linear discriminant and LDA are often used interchangeably, although Fisher's original article[1] actually describes a slightly different discriminant, which does not make some of the assumptions of LDA such as normally distributed classes or equal class covariances.
Suppose two classes of observations have means  and covariances
and covariances 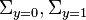 . Then the linear combination of features
. Then the linear combination of features 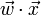 will have means
will have means 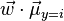 and variances
and variances  for
for  . Fisher defined the separation between these two distributions to be the ratio of the variance between the classes to the variance within the classes:
. Fisher defined the separation between these two distributions to be the ratio of the variance between the classes to the variance within the classes:
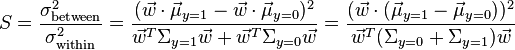
This measure is, in some sense, a measure of the signal-to-noise ratio for the class labelling. It can be shown that the maximum separation occurs when

When the assumptions of LDA are satisfied, the above equation is equivalent to LDA.
Be sure to note that the vector  is the normal to the discriminant hyperplane. As an example, in a two dimensional problem, the line that best divides the two groups is perpendicular to
is the normal to the discriminant hyperplane. As an example, in a two dimensional problem, the line that best divides the two groups is perpendicular to  .
.
Generally, the data points to be discriminated are projected onto  ; then the threshold that best separates the data is chosen from analysis of the one-dimensional distribution. There is no general rule for the threshold. However, if projections of points from both classes exhibit approximately the same distributions, a good choice would be the hyperplane between projections of the two means,
; then the threshold that best separates the data is chosen from analysis of the one-dimensional distribution. There is no general rule for the threshold. However, if projections of points from both classes exhibit approximately the same distributions, a good choice would be the hyperplane between projections of the two means,  and
and  . In this case the parameter c in threshold condition
. In this case the parameter c in threshold condition  can be found explicitly:
can be found explicitly:
 .
.