Details view: Quadratic unconstrained binary optimization (QUBO)

Quadratic unconstrained binary optimization (QUBO) Komponentas1 #306148 Quadratic unconstrained binary optimization (QUBO) is a pattern matching technique, common in machine learning applications. QUBO is an NP hard problem. QUBO problems are particularly well suited for processing on quantum computers.
QUBO is given by the formula: 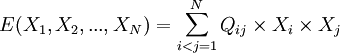$E(X_1, X_2, ... , X_N) = \sum_{i<j=1}^N Q_{ij} \times X_i \times X_j$ Abstract Quadratic Unconstrained Binary Optimization (QUBO) problems concern the minimization of quadratic polynomials in n{0,1}-valued variables. These problems are NP-complete, but prior work has identified a sequence of polynomial-time computable lower bounds on the minimum value, denoted by C₂,C₃,C₄,…. It is known that C₂ can be computed by solving a maximum flow problem, whereas the only previously known algorithms for computing require solving a linear program. In this paper we prove that C₃ can be computed by solving a maximum multicommodity flow problem in a graph constructed from the quadratic function. In addition to providing a lower bound on the minimum value of the quadratic function on {0,1}ⁿ, this multicommodity flow problem also provides some information about the coordinates of the point where this minimum is achieved. By looking at the edges that are never saturated in any maximum multicommodity flow, we can identify relational persistencies: pairs of variables that must have the same or different values in any minimizing assignment. We furthermore show that all of these persistencies can be detected by solving single-commodity flow problems in the same network. Keywords Quadratic unconstrained binary optimization; Multicommodity flow; Network flow; Persistency; Roof duality 1. Introduction In this paper, we study the problem of Quadratic Unconstrained Binary Optimization (QUBO), which determines the minimum over {0,1}ⁿ of quadratic pseudo-Boolean functions of the form Turn MathJaxon Quadratic pseudo-Boolean functions are a common class of energy functions that are widely useful, and which have been strikingly successful in computer vision (see [7] for a recent survey). Even in cases when the QUBO problem cannot be fully solved by an efficient algorithm, one can often extract useful information for the computer vision applications by discovering persistencies, i.e. partial assignments of the variables that must occur in an assignment that minimizes the function. Persistencies have proved to be particularly useful for medical imaging applications [9]. Although the QUBO problem is NP-hard, several approaches have been proposed to give good lower bounds on the minimum value. Many of these approaches involve rewriting the quadratic pseudo-Boolean function using posiforms, which we now define. Let V={x₁,x₂,…,x_n} be the set of variables, and let denote the set of negated variables, where . The elements of are called literals. We can represent non-negative pseudo-Boolean functions as posiforms, i.e. multilinear polynomial expressions over all the literals with positive term coefficients Turn MathJaxon where Ω is a collection of subsets of L, and a_T>0 for all T∈Ω. Every posiform ϕ defines a unique pseudo-Boolean function f on substituting , but a pseudo-Boolean function can have multiple posiform representations. A particular lower bound called the roof-dual, denoted by C₂, is introduced in [8]. If f is a quadratic pseudo-Boolean function, then C₂ is the maximum c such that f=c+ϕ, where ϕ is a posiform of degree 2. It is shown in [6] that we can compute C₂ by solving a maximum flow problem on a special graph called an implication network. The roof-dual value is then generalized to a family of lower bounds C_k. (See [2] for definitions.) In this paper we will focus on the bound C₃. Let P₃ be the cone of non-negative quadratic pseudo-Boolean functions having a posiform of degree 3. Then as defined in [3] C₃=max{c∈R\|f=c+ϕ,ϕ∈P₃}. Turn MathJaxon It is proved in [3] that C₃ can be computed by solving an odd cycle packing problem, but due to the fact that C₂ can be computed using maximum flow, we are interested in formulating C₃ as the solution of a flow problem. Among the set of all possible posiforms of a quadratic pseudo-Boolean function, we will work with the bi-formin particular, which is introduced in [4]. For variables x and y, we call a positive bi-term, and a negative bi-term. If E denotes a collection of bi-terms such that no pair of variables is involved in more than one element of E, and α_e>0 for all e∈E, then we call ϕ=∑_e∈Eα_ee a bi-form. By introducing variable x₀, we can write any quadratic pseudo-Boolean function f in variables x₁,…,x_n uniquely as f(x₁,…,x_n)=c_f+ϕ_f(1,x₁,…,x_n), where ϕ_f is a bi-form in the variables x₀,x₁,…,x_n. (See [5].) Given a quadratic pseudo-Boolean function f=c_f+ϕ_f, where ϕ_f is a bi-form, we define an undirected graphG_{ϕ_f}=(V_{ϕ_f},E_{ϕ_f}) as follows. V_{ϕ_f}=L, where L is the set of literals of f. We associate two edges with each bi-term. For positive bi-term , we have edges (x_i,x_j) and , with weight . For negative bi-term , we have edges and , with weight . Conversely, edge (u,v) with capacity δ in G_{ϕ_f} corresponds to the bi-term . We prove in Section 3 that for any quadratic pseudo-Boolean function f, C₃ is the sum of c_f and the maximum multicommodity flow value of network G_{ϕ_f} with source–sink pairs . (See Section 2 for definitions related to multicommodity flow.) Besides being helpful to have the numerical lower bound on the minimum value, it is also useful to obtain partial optimal assignments. The concepts of persistency and autarky are defined in [6], and we can generalize the idea of persistency and autarky to relational persistency and relational autarky. Call a set of literals valid if it contains at most one of x_i and for all i. Consider a valid subset U∈L. We will say U is astrong (resp., weak) relational persistency if literals in U have the same value in all (resp., some) optimal assignment. For any assignment x=(x₁,…,x_n) and Boolean value b∈{0,1}, let x[U→b] denote the assignmenty=(y₁,…,y_n) specified by Turn MathJaxon We will call U a strong (resp., weak) relational autarky if for all Boolean assignments x, there exists a value b∈{0,1} such that f(x[U→b])<f(x) (resp., f(x[U→b])≤f(x)), or x[U→b]=x. Relational persistencies and relational autarkies allow us to reduce the size of the optimization problem, since we can rewrite a posiform with a smaller variable set, while maintaining the same minimum value. In Section 4, we focus on finding strong relational persistencies. When we push flow along a path in G_{ϕ_f} fromx_i to , it is equivalent to rewriting the bi-terms associated with edges on the path into a cubic posiform, and it turns out that we can derive strong relational persistencies from the residual graph. In Theorem 2, we prove that if an edge (u,v) can never be saturated in a solution of our maximum multicommodity flow problem, literals u and v must have the same value in any minimizer of f. Then in Theorem 3, we consider the maximum flow problem on G_{ϕ_f} with single source–sink pair , and we show that in the residual graph, the set of literals in the connected component containing x_i is a strong relational persistency. Furthermore, we show that if U is a strong relational persistency, and x_i∈U, then there must be a maximum flow assignment for source–sink pair such that U is a connected component in the residual graph. Unsurprisingly, many techniques used in studying C₃ generalize those used in studying C₂. We introduce the variable x₀ simply to make the posiform homogeneously quadratic, and we don’t treat x₀ differently in computing C₃ and deriving relational persistencies. Various known facts about C₂ and its associated persistencies can be interpreted as a special case of the facts derived here, when we enforce the constraintx₀=1. For example, [6] obtains strong relational autarkies from the residual graph of running a maximum flow computation for the source–sink pair . In Theorem 3, we use the same technique over all source–sink pairs . 2. Definitions and notation In this section, we summarize some definitions and notation involving multicommodity flow problems and their relationship to quadratic Boolean formulas. 2.1. Weighted signed graphs, odd cycles A weighted signed graph G is an undirected graph (V,E) together with a set of positive weights {α_e\|e∈E}and a partition {E⁺,E⁻} of the edge set E. The edges in E⁺ are called positive, and those in E⁻ are called negative. A cycle of G is called odd if it contains an odd number of negative edges. The set of odd cycles is denoted by C. 2.2. Odd cycle packing Given weighted signed graph G, the odd cycle packing problem (CP) is equation1 Turn MathJaxon Turn MathJaxon Turn MathJaxon 2.3. Multicommodity flow Given undirected graph G=(V,E) with edge capacities c_e≥0, and source–sink pairs (s₁,t₁),…,(s_k,t_k), let . ³The maximum multicommodity flow problem on G is equation2 Turn MathJaxon Turn MathJaxon Turn MathJaxon Any vector (ζ_p) satisfying the constraints in (2) is called a multicommodity flow, or simply a flow, regardless of whether it maximizes the objective function. For a thorough introduction to multicommodity flow theory, we refer the reader to [1]. 2.4. The graphs G_f and G_ϕ Given quadratic pseudo-Boolean function f, we can write f uniquely as the sum of a constant and a bi-form: f=c_f+ϕ_f. Turn MathJaxon We can construct a weighted signed graph G_f=(V_f,E_f) corresponding to bi-form ϕ_f as follows. The vertex set V_f is equal to {x₀,…,x_n}, the set of variables of ϕ_f. We associate an edge with each bi-term in ϕ_f. Edges have the same sign as their associated bi-terms, and the weights α_e are the same as the coefficients of their associated bi-terms. Recall that there is another graph associated with ϕ_f, namely the graph G_{ϕ_f} with vertex set defined in Section 1. Henceforth we will use the notation G_ϕ rather than G_{ϕ_f} for convenience. In Section 3 we will relate the maximum multicommodity flow problem in G_ϕ to the odd cycle packing problem in G_f. 2.5. Symmetric flow The graph G_ϕ has a twofold symmetry given by a permutation ι:V_ϕ→V_ϕ. This permutation is defined by setting and . We can extend ι to edges in the obvious way: if u,v are literals and e=(u,v) is an edge of G_ϕ, then the definition of G_ϕ ensures that is also an edge of G_ϕ and we can define . Similarly we can extend ι to sets of vertices — ι(S)={u\|ι(u)∈S} — and to paths: for a path p in G_ϕ, if p=v₁→⋯→v_k then ι(p)=ι(v_k)→⋯→ι(v₁). (Note that ι reverses the direction of the path.) Finally we can extend ι to flows: if ζ is any flow, then ι(ζ) is defined by setting ι(ζ)_p=ζ_ι(p) for all paths p. Note that ι(ζ) is also a flow because the edge capacities are preserved by ι. A flow ζ is calledsymmetric if it satisfies ι(ζ)=ζ. Note that if ζ is any maximum multicommodity flow, then is also a maximum multicommodity flow, and it is symmetric. Thus, there is always at least one symmetric flow that optimizes (2). 3. Computing C₃ reduces to multicommodity flow Give quadratic pseudo-Boolean function f, we can find its unique bi-form representation, f=c_f+ϕ_f, then construct G_f and G_ϕ according to ϕ_f. Denote by v(CP) the optimal value of the cycle packing problem onG_f, and by v(PP) the optimal value of the multicommodity flow problem on G_ϕ with source–sink pairs . Lemma 1. For any quadratic pseudo-Boolean functionf,C₃=c_f+v(CP). Proof. See [3]. □ Lemma 2. For any quadratic pseudo-Boolean functionf,v(PP)=v(CP). Proof. To prove Lemma 2, we will show that for every feasible solution ξ of the cycle packing problem, we can construct a feasible symmetric solution ζ of the multicommodity flow problem with the same objective function value, and vice versa.ξ→ζ:Given odd cycle C∈C, starting from the variable with the lowest index, we can derive two paths p_C and in G_f where Turn MathJaxon Turn MathJaxon For every path p in G_f, there is a unique path λ(p)=u₀→⋯→u_k+1 in G_ϕ satisfying u₀=x_c₀, and for all i>0. In fact λ(p) can be defined by letting p[1..i] denote the initial segment of pstarting at x_c₀ and ending at x_{c_i}, and setting Turn MathJaxon Note that when p is an odd cycle.Given feasible CP solution ξ, we can construct solution ζ of the multicommodity flow problem: Turn MathJaxon It is clear that ξ and ζ have the same objective function value, and ζ is symmetric. The flow ζ is also feasible, because if ζ violates the capacity constraint of edge (u,v) in PP, ξ must violate the corresponding constraint of the edge in CP. Here and henceforth, var denotes the function from literals to variables defined by .ζ→ξ:Given path p∈P_i in G_ϕ, we can write pas Turn MathJaxon Extending the function var to paths, we get paths in G_f: Turn MathJaxon Consider V_ϕ as the union of two sets V_f and . An easy observation is that if an edge’s two endpoints are in the same set, its associated bi-term is positive, and if its endpoints are in different sets, it is associated with a negative bi-term. Since p goes from x_i to , we know that there are an odd number of edges in p that are associated with negative bi-terms, so . Given a feasible solution ζ of the multicommodity flow problem, we can construct a solution ξ of the cycle packing problem: Turn MathJaxon ξ has the same objective function value as ζ. We can prove that ξ is feasible by contradiction.Suppose ξviolates the constraint Turn MathJaxon Each edge in E_f is associated with a bi-term, which corresponds to two edges in E_ϕ, so for edge e₀ there are two corresponding edges e₁,e₂∈E_ϕ, where Turn MathJaxon From the correspondence between paths in G_ϕ and odd cycles in G_f, we know that every path p with must use one of e₁ and e₂, so Turn MathJaxon Turn MathJaxon Turn MathJaxon We know that at least one of the two constraints in multicommodity flow is violated, i.e., Turn MathJaxon Turn MathJaxon which contradicts the feasibility of ζ. Thus we know that ξ must be feasible.Since for every feasible solution ξ of cycle packing problem, we can construct a feasible solution ζ of the multicommodity flow problem with the same objective function value, and vice versa, v(CP)=v(PP). □ Theorem 1. For any quadratic pseudo-Boolean functionf,C₃=c_f+v(PP). Proof. Theorem 1 is a direct result of Lemma 1 and Lemma 2. □ 4. Persistency and autarky results Theorem 2. Ife=(u,v)is an edge ofG_ϕsuch thateis not saturated in any symmetric maximum multicommodity flow, then{u,v}is a strong relational persistency for the corresponding pseudo-Boolean functionf. Proof. Notice that given a feasible solution ζ for the multicommodity flow problem on G_ϕ, we can express the graph’s edge capacity vector as the sum of two non-negative vectors, one for the flow value on edges, and the other for the remaining edge capacities. We refer to these vectors as “the flow layer” and “the remaining graph layer”. The flow layer can be directly derived from the flow assignments, and the remaining graph layer,G_ϕ,ζ=(V_ϕ,ζ,E_ϕ,ζ), where: • V_ϕ,ζ=V_ϕ. • E_ϕ,ζ={e∈E_ϕ∣c_e>∑_i∑_{p∈P_i,P∋e}ζ_p}. • For all e∈E_ϕ,ζ, the capacity is c_e,ζ=c_e−∑_i∑_{p∈P_i\|P∋e}ζ_p. We will make use of the following lemma from [3]. Lemma 3.. Proof. Lemma 3 can be easily proven by induction. See [3] for a proof. □ Using Lemma 3, we can transform a flow along path with value δ to the sum of a constant and a cubic posiform: Turn MathJaxon It follows that the flow layer can be written as the sum of a constant — which is equal to the flow value — and a homogeneous cubic Boolean function, while the remaining graph layer corresponds to a homogeneous quadratic Boolean function.Suppose e=(u,v) is never saturated in any optimal symmetric multicommodity flow solution. Among all optimal solutions, consider those with the maximum number of vertices in the component containing v in the graph G_ϕ,ζ, and among these solutions, let ζ be the one with the minimum c_e,ζ. By our assumption on ζ, if we maintain the same total flow value, it will be impossible to expand the connected component containing v, and it is also impossible to decrease c_e,ζwithout making the component containing v smaller. Suppose there exists an optimal assignment x^∗ withu≠v. Without loss of generality, we can assume that x^∗ assigns u=0 and v=1.Define S to be the set of vertices of the connected component containing v in the subgraph induced by vertices with value 1 according to x^∗ in G_ϕ,ζ. We will show that changing the values of literals in S to 0, and their negations to 1, will give an assignment x^′ such that , thus contradicting the hypothesis that x^∗ is an optimal assignment.Write the pseudo-Boolean function f as the sum of constant, cubic terms corresponding to the flow solution ζ, and quadratic terms corresponding to G_ϕ,ζ. An easy observation is that setting the two endpoints of an edge to the same value will give the corresponding bi-term value 0. It is then easy to see that x^′ will decrease the value of quadratic terms by at least c_e,ζ. Now if we can show that changing from x^∗ to x^′ will not increase the value of cubic terms, then we know that will be strictly less than . Lemma 4. Given symmetric flow assignmentζ₁, for pathpfromx_itowith flow value(ζ₁)_p>0, and vertexx_j≠x_i, ifx_joris onp, or there exists a simple pathp^′inG_ϕ,ζ₁fromx_jorto any vertex onp, we can get a flow assignmentζ₂such that: 1. ζ₁andζ₂have the same flow value, 2. E_ϕ,ζ₁⊆E_ϕ,ζ₂, 3. ife^′=(u^′,v^′)belongs top^′but notp,ζ₂puts more flow one^′thanζ₁does, andc_e^′,ζ₂<c_e^′,ζ₁, 4. ife^′=(u^′,v^′)is not inp,c_e^′,ζ₂≤c_e^′,ζ₁. Proof. Since ζ₁ is symmetric, a flow along path implies a flow along path with the same value. The two paths together will then form a generalized cycle, which we define to be a walk that starts and ends at the same vertex, but may traverse an edge more than once. If x_j or is on p, we can cut the cycle into two possibly non-simple paths at x_j and , then take some shortcuts to make the two paths simple. For example, consider Turn MathJaxon Turn MathJaxon Then redistributing the flow as from u₂ to will give Turn MathJaxon Turn MathJaxon Notice that the redistribution operation may increase some edges’ remaining capacities. In the above example, the remaining capacities of c_{(x_i,u₁),ζ} and are increased. If an edge is not on p, then its remaining capacity will not be increased.If there exists a simple path from x_j or to some v^′ on p, we only need to consider the first case, since by symmetry the second case will be equivalent to the first one if we switch p and ι(p). Without loss of generality, assume that the path p_e from x_j to v^′ uses no edge on p or ι(p); otherwise we can take a different v^′ and get a shorter p_e. We can first redistribute the flow as from v^′ to without increasing the remaining capacity of any edge on p_e, then extend a small portion of the flow δ^′ as from x_j to using p_e and ι(p_e). If we make δ^′ small enough, the redistribution will not saturate any edge on p_e and ι(p_e). □ Lemma 5. All paths involving vertices inSwith positive flow value must use the edge(u,v)or. Proof. Suppose there is flow along p passing v^′∈S without using (u,v) and . Since there exist pathsu→v→v^′ and in G_ϕ,ζ, we know from Lemma 4 that we can get another optimal flow assignment without shrinking the connected component containing v, but decrease c_(u,v),ζ, which contradicts our assumption about ζ. □ Lemma 5 implies that all flows involving the literals with different values in x^′ and x^∗ are along paths using the (undirected) edge (u,v) or . Since p and ι(p) yield the same function terms, and p uses implies ι(p) uses (u,v), we only need to prove that x^′ will not increase the value of the cubic terms corresponding to the flow along paths using (u,v). Since all such paths use vertex u, we can redistribute the flows as from u to . We will no longer assume the minimality of c_(u,v),ζ, since the redistribution may increase c_(u,v),ζ.By Lemma 3, we know that the cubic terms corresponding to these flow paths all have the form Turn MathJaxon which can be further reduced to quadratic terms by the assumption u=0: Turn MathJaxon Consider any specific flow path. When we change x^∗ to x^′, there are only two cases in which the value of the above expression can be increased:The first case is v_ℓ=1 in x^′, and v_ℓ+1∈S. Then the term has value 0 according to x^∗, but value 1 according to x^′. The second case is the symmetric counterpart of the first case, namely v_ℓ∈ι(S), and v_ℓ+1=0 in x^′. If we can prove that the first case is impossible, by symmetry the second case is also impossible.Suppose we have the first case in the flow along path p. By the fact that v_ℓ=1 in x^′, we know that v_ℓ∉S. If v_ℓ∈ι(S), the edge (v_ℓ,v_ℓ+1) must be saturated, since otherwise there exists a path from u to in G_ϕ,ζ, contradicting our assumption that ζis a maximum flow. If v_ℓ∉ι(S), v_ℓ=1 in x^∗, and by the definition of S, v_ℓ∉S implies that the edge(v_ℓ,v_ℓ+1) is saturated. Either way, (v_ℓ,v_ℓ+1) is saturated. Furthermore, since v_ℓ+1 is in S, there exists a path from v to v_ℓ+1 in G_ϕ,ζ that does not use edge (v_ℓ,v_ℓ+1). Hence we can reroute some small enough portion of the original flow to use the alternative path from v to v_ℓ+1, thus making the edge(v_ℓ,v_ℓ+1) unsaturated without changing the value of the flow solution. This will enlarge S to S∪{v_ℓ}, contradicting the maximality of S.By the above discussion, we know that x^′ won’t increase the value of the cubic terms, and will decrease the value of the quadratic terms by at least c_(u,v),ζ. This contradicts the optimality of x^∗, so u and v must have the same value in any optimal assignment. □ 4.1. Persistencies and autarkies from single-commodity flows Lemma 6. Any subset of a strong relational autarky is a strong relational persistency. Proof. Suppose S is a subset of some strong relational autarky S^′. Consider any optimal assignment x. Since it is not possible to have f(x[S^′→b])<f(x), it must be the case that x assigns the same value to all literals in S^′. Since S⊆S^′, all literals in S have the same value in all optimal assignments, which makes S a strong relational persistency. □ Consider any symmetric optimal solution ζ of the single-commodity maximum flow problem with source x_sand sink on G_ϕ. Using the same definition of G_ϕ,ζ as in the proof of Theorem 2, let S denote the connected component containing x_s in G_ϕ,ζ. Theorem 3. Sis a strong relational persistency of the corresponding pseudo-Boolean functionf. Conversely, ifUis a strong relational persistency containingx_i, then there exists a symmetric optimal assignmentζof the single-commodity flow problem with source–sink pair, such thatUis completely contained in the connected component containingx_iinG_ϕ,ζ. Proof. We will start with the first part of the theorem. Notice that S contains at most one of x_i and for all i, since otherwise symmetry implies a path from x_s to in G_ϕ,ζ.First consider the case when ζ is a maximum flow assignment such that the set S is maximal. If S has at most one element, then S is a strong relational autarky by definition. Otherwise, consider any assignment x, and assume that two literals in S have different values according to x. Let b=0. We shall prove f(x[S→b])<f(x), from which it follows that S is a strong relational autarky.Let K=S∪ι(S). Write f as the sum of a constant, cubic terms corresponding to flow solution ζ, and quadratic terms corresponding to G_ϕ,ζ. We will show that in this expression for f, all terms involving literals in K will have value 0 according to x[S→b]. Consider any quadratic term involving literals inK. The term must correspond to edges in G_ϕ,ζ whose endpoints are both in S or both in ι(S), since there is no edge between S and V_ϕ,ζ∖S. The term will vanish, since the endpoints of its corresponding edge are set to the same value in x[S→b].For the cubic terms, since all flows are from x_s to , using Lemma 3, we know that the cubic terms all have the form Turn MathJaxon We have x_s=b=0 in x[S→b], so the cubic terms can be reduced to Turn MathJaxon Consider any term in the above formula involving variables in K. Like for the proof of Theorem 2, there are only two cases such that the term will not vanish. The first case is v_ℓ=1, and v_ℓ+1∈S. Then the term has value 1 according to x[S→b]. The second case is the symmetric counterpart of the first case, namely v_ℓ∈ι(S), and v_ℓ+1=0. If we can prove that the first case is impossible, by symmetry the second case is also impossible. Using the same argument as in proof of Theorem 2, if the first case happens, we can expand S without changing the total flow value, thus contradicting the maximality of S. So all terms involving literals in K will vanish.S is a strong relational autarky for the following reason. Terms not using literals in K will have the same value with respect to x and x[S→b], and all terms using literals in K will vanish under x[S→b]. Moreover, since there exist two literals in S that are assigned different values by x, and the two literals are connected in G_ϕ,ζ, at least one term using literals in K will not vanish under x, implying f(x[S→b])<f(x).Now consider an arbitrary maximum flow solution ζ without assuming S to be maximal. The only difference from the above case is that we can expand S by rerouting flows. It is clear that the new value of S after the expansion will be a superset of the former value of S. Thus starting from an arbitrary ζ and S, we can always get another maximum flow assignment ζ^′ with a maximal S^′, and S⊆S^′, where S^′ is a strong relational autarky. By Lemma 6, we know that S is a strong relational persistency.Now we prove the second part of the theorem. Let ζ be the maximum single-commodity flow assignment with a maximal connected component containing x_i, and denote the connected component by S. Recall that we assume U to be a strong relational persistency containingx_i.The proof is by contradiction. Assuming U⊈S, we get a partition {U₁,U₂} of U where U₂=U∖S, and U₁=U∩S. U₂ is non-empty since U⊈S, and U₁ is also non-empty since x_i∈U₁. By definition of strong relational persistency, literals in U₁ and U₂ must have the same value in all optimal assignments. Consider an optimal assignment x^∗. We can assume that all literals in U₁ and U₂ have value 1 in x^∗, since the bi-form will have the same function value if we negate all variables’ values. By the discussion from the first part of the proof, we know that x^∗[S→0] must also be an optimal assignment, where literals inU₁ have value 0, and literals in U₂ have value 1. The optimality of x^∗[S→0] contradicts the assumption that U is a strong relational persistency; thus U⊆S. □ Notice that if U is a strong relational persistency, then ι(U) is also a strong relational persistency, and they are semantically equivalent, so a strong relational persistency containing implies an equivalent strong relational persistency containing x_i. Theorem 3 then suggests that we can derive all strong relational persistencies by computing single-commodity maximum flows in G_ϕ. The reverse direction ofTheorem 3 also suggests that if S={u,v} is derived from Theorem 2 as a strong relational persistency, then it can also be derived from Theorem 3 as a subset of a strong relational autarky. Remark. The forward direction of Theorem 3 follows from remarks in [4], and the preprocessing code in [6]also applied the idea. The reverse direction is new, and guarantees that we can derive all strong relational persistencies using single-commodity maximum flows. Acknowledgments The authors wish to thank Ramin Zabih for introducing us to this topic and for providing valuable guidance along the way. We also thank Endre Boros for many valuable discussions and observations about our research and related work. References [1] R.K. Ahuja, T.L. Magnanti, J.B. Orlin Network Flows: Theory, Algorithms, and Applications Prentice Hall (1993) [2] E. Boros, Y. Crama, P.L. Hammer Upper-bounds for quadratic 0-1 maximization Operations Research Letters, 9 (2) (1990), pp. 73–79 Article \| PDF (427 K) \| View Record in Scopus \| Cited By in Scopus (16) [3] E. Boros, Y. Crama, P.L. Hammer Chvatal cuts and odd cycle inequalities in quadratic 0-1 optimization SIAM Journal on Discrete Mathematics, 5 (2) (1992), pp. 163–177 Full Text via CrossRef [4] E. Boros, P.L. Hammer, A max-flow approach to improved roof-duality in quadratic 0-1 minimization, Research Report 15, Rutgers Center for Operations Research, Rutgers University, New Brunswick, NJ, 1989 [5] E. Boros, P.L. Hammer, R. Sun, G. Tavares A max-flow approach to improved lower bounds for quadratic 0-1 minimization Discrete Optimization, 5 (2) (2008), pp. 501–529 Article \| PDF (675 K) \| View Record in Scopus \| Cited By in Scopus (17) [6] E. Boros, P.L. Hammer, G. Tavares, Preprocessing of unconstrained quadratic binary optimization, Research Report 10, Rutgers Center for Operations Research, Rutgers University, New Brunswick, NJ, 2006 [7] P. Felzenszwalb, R. Zabih, An overview of graph algorithms and dynamic programming in computer vision, IEEE Transactions in Pattern Analysis and Machine Intelligence, in press [8] P.L. Hammer, P. Hansen, B. Simeone Roof duality, complementation and persistency in quadratic 0-1 optimization Mathematical Programming, 28 (2) (1984), pp. 121–155 View Record in Scopus \| Full Text via CrossRef \| Cited By in Scopus (123) [9] A. Raj, G. Singh, R. Zabih, B. Kressler, Y. Wang, N. Schuff, M. Weiner Bayesian parallel imaging with edge-preserving priors Magnetic Resonance in Medicine, 57 (1) (2007), pp. 8–21 View Record in Scopus \| Full Text via CrossRef \| Cited By in Scopus (29) Corresponding author. Tel.: +1 607 379 1538; fax: +1 607 255 4428. 1 Partially supported by NSF Grant IIS-0803705 and NIH Grant P41RR023953. 2 Supported by the National Science Foundation (grants CCF-0643934 and CCF-0729102), the Air Force Office of Scientific Research, an Alfred P. Sloan Foundation Fellowship, and a Microsoft Research New Faculty Fellowship. 3 Throughout this paper, we work with undirected graphs and make no distinction between a path and its reverse. In particular, a path from s to t is also a path from t to s. Copyright © 2009 Elsevier B.V. Published by Elsevier B.V. All rights reserved.

Immediately related elementsHow this works

-

Machine Learning Methods & Algorithms »

▲

Others »

■

Quadratic unconstrained binary optimization (QUBO)

Heading

Summary

Details

Lock

+Komentarai (0)

+Citavimą (0)

+About