Q-learning is a model-free reinforcement learning technique. Specifically, Q-learning can be used to find an optimal action-selection policy for any given (finite) Markov decision process (MDP). It works by learning an action-value function that ultimately gives the expected utility of taking a given action in a given state and following the optimal policy thereafter. When such an action-value function is learned, the optimal policy can be constructed by simply selecting the action with the highest value in each state. One of the strengths of Q-learning is that it is able to compare the expected utility of the available actions without requiring a model of the environment. Additionally, Q-learning can handle problems with stochastic transitions and rewards, without requiring any adaptations. It has been proven that for any finite MDP, Q-learning eventually finds an optimal policy.
Contents
[hide] - 1 Algorithm
- 2 Influence of variables on the algorithm
- 2.1 Learning rate
- 2.2 Discount factor
- 2.3 Initial conditions ()
- 3 Implementation
- 4 Early study
- 5 Variants
- 6 See also
- 7 External links
- 8 References
Algorithm[edit]
The problem model, the MDP, consists of an agent, states S and a set of actions per state A. By performing an action 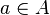 , the agent can move from state to state. Each state provides the agent a reward (a real or natural number). The goal of the agent is to maximize its total reward. It does this by learning which action is optimal for each state.
, the agent can move from state to state. Each state provides the agent a reward (a real or natural number). The goal of the agent is to maximize its total reward. It does this by learning which action is optimal for each state.
The algorithm therefore has a function which calculates the Quality of a state-action combination:

Before learning has started, Q returns an (arbitrary) fixed value, chosen by the designer. Then, each time the agent selects an action, and observes a reward and a new state that both may depend on both the previous state and the selected action. The core of the algorithm is a simple value iteration update. It assumes the old value and makes a correction based on the new information.
![Q_{t+1}(s_{t},a_{t}) = \underbrace{Q_t(s_t,a_t)}_{\rm old~value} + \underbrace{\alpha_t(s_t,a_t)}_{\rm learning~rate} \times \left[ \overbrace{\underbrace{R_{t+1}}_{\rm reward} + \underbrace{\gamma}_{\rm discount~factor} \underbrace{\max_{a}Q_t(s_{t+1}, a)}_{\rm estimate~of~optimal~future~value}}^{\rm learned~value} - \underbrace{Q_t(s_t,a_t)}_{\rm old~value} \right]](http://upload.wikimedia.org/math/6/a/d/6ad8413f646925386a150e5d3deb6c91.png)
where  is the reward observed after performing
is the reward observed after performing 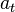 in
in 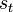 , and where
, and where  (
( ) is the learning rate (may be the same for all pairs). The discount factor
) is the learning rate (may be the same for all pairs). The discount factor  (
( ) trades off the importance of sooner versus later rewards.
) trades off the importance of sooner versus later rewards.
An episode of the algorithm ends when state 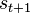 is a final state (or, "absorbing state"). However, Q-learning can also learn in non-episodic tasks. If the discount factor is lower than 1, the action values are finite even if the problem can contain infinite loops.
is a final state (or, "absorbing state"). However, Q-learning can also learn in non-episodic tasks. If the discount factor is lower than 1, the action values are finite even if the problem can contain infinite loops.
Note that for all final states  ,
, 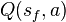 is never updated and thus retains its initial value. In most cases,
is never updated and thus retains its initial value. In most cases, 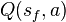 can be taken to be equal to zero.
can be taken to be equal to zero.
Influence of variables on the algorithm[edit]
Learning rate[edit]
The learning rate determines to what extent the newly acquired information will override the old information. A factor of 0 will make the agent not learn anything, while a factor of 1 would make the agent consider only the most recent information. In fully deterministic environments, a learning rate of 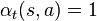 is optimal. When the problem is stochastic, the algorithms still converges under some technical conditions on the learning rate, that require it to decrease to zero. In practice, often a constant learning rate is used, such as
is optimal. When the problem is stochastic, the algorithms still converges under some technical conditions on the learning rate, that require it to decrease to zero. In practice, often a constant learning rate is used, such as 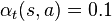 for all
for all  .[1]
.[1]
Discount factor[edit]
The discount factor determines the importance of future rewards. A factor of 0 will make the agent "myopic" (or short-sighted) by only considering current rewards, while a factor approaching 1 will make it strive for a long-term high reward. If the discount factor meets or exceeds 1, the action values may diverge.
Initial conditions (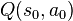 )[edit]
)[edit]
Since Q-learning is an iterative algorithm, it implicitly assumes an initial condition before the first update occur. A high (infinite) initial value, also known as "optimistic initial conditions",[2] can encourage exploration: no matter what action will take place, the update rule will cause it to have lower values than the other alternative, thus increasing their choice probability. Recently, it was suggested that the first reward  could be used to reset the initial conditions. According to this idea, the first time an action is taken the reward is used to set the value of
could be used to reset the initial conditions. According to this idea, the first time an action is taken the reward is used to set the value of 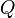 . This will allow immediate learning in case of fix deterministic rewards. Surprisingly, this resetting-of-initial-conditions (RIC) approach seems to be consistent with human behaviour in repeated binary choice experiments.[3]
. This will allow immediate learning in case of fix deterministic rewards. Surprisingly, this resetting-of-initial-conditions (RIC) approach seems to be consistent with human behaviour in repeated binary choice experiments.[3]
Implementation[edit]
Q-learning at its simplest uses tables to store data. This very quickly loses viability with increasing levels of complexity of the system it is monitoring/controlling. One answer to this problem is to use an (adapted) artificial neural network as a function approximator, as demonstrated by Tesauro in his Backgammon playing temporal difference learning research.[4]
More generally, Q-learning can be combined with function approximation.[5] This makes it possible to apply the algorithm to larger problems, even when the state space is continuous, and therefore infinitely large. Additionally, it may speed up learning in finite problems, due to the fact that the algorithm can generalize earlier experiences to previously unseen states.
Early study[edit]
Q-learning was first introduced by Watkins[6] in 1989. The convergence proof was presented later by Watkins and Dayan[7] in 1992.
Variants[edit]
Delayed Q-learning is an alternative implementation of the online Q-learning algorithm, with Probably approximately correct learning (PAC).[8]
Due to the fact that the maximum approximated action value is used in the Q-learning update, in noisy environments Q-learning can sometimes overestimate the actions values, slowing the learning. A recent variant called Double Q-learning was proposed to correct this. [9]
Greedy GQ is a variant of Q-learning to use in combination with (linear) function approximation.[10] The advantage of Greedy GQ is that convergence guarantees can be given even when function approximation is used to estimate the action values.
See also[edit]
External links[edit]
- Watkins, C.J.C.H. (1989). Learning from Delayed Rewards. PhD thesis, Cambridge University, Cambridge, England.
- Strehl, Li, Wiewiora, Langford, Littman (2006). PAC model-free reinforcement learning
- Q-Learning by Examples
- Reinforcement Learning: An Introduction by Richard Sutton and Andrew S. Barto, an online textbook. See "6.5 Q-Learning: Off-Policy TD Control".
- Connectionist Q-learning Java Framework
- Piqle: a Generic Java Platform for Reinforcement Learning
- Reinforcement Learning Maze, a demonstration of guiding an ant through a maze using Q-learning.
- Q-learning work by Gerald Tesauro
- Q-learning work by Tesauro Citeseer Link
- Q-learning algorithm implemented in processing.org language
References[edit]
- Jump up^ Reinforcement Learning: An Introduction. Richard Sutton and Andrew Barto. MIT Press, 1998.
- Jump up^ http://webdocs.cs.ualberta.ca/~sutton/book/ebook/node21.html
- Jump up^ The Role of First Impression in Operant Learning. Shteingart H, Neiman T, Loewenstein Y. J Exp Psychol Gen. 2013 May; 142(2):476-88. doi: 10.1037/a0029550. Epub 2012 Aug 27.
- Jump up^ Tesauro, Gerald (March 1995). "Temporal Difference Learning and TD-Gammon". Communications of the ACM 38 (3). Retrieved 2010-02-08.
- Jump up^ Hado van Hasselt. Reinforcement Learning in Continuous State and Action Spaces. In: Reinforcement Learning: State of the Art, Springer, pages 207-251, 2012
- Jump up^ Watkins, C.J.C.H., (1989), Learning from Delayed Rewards. Ph.D. thesis, Cambridge University.
- Jump up^ Watkins and Dayan, C.J.C.H., (1992), 'Q-learning.Machine Learning', ISBN : 8:279-292
- Jump up^ Alexander L. Strehl, Lihong Li, Eric Wiewiora, John Langford, and Michael L. Littman. Pac model-free reinforcement learning. In Proc. 23nd[clarification needed] ICML 2006, pages 881–888, 2006.
- Jump up^ Hado van Hasselt. Double Q-learning. In Advances in Neural Information Processing Systems 23, pages 2613-2622, 2011.
- Jump up^ Hamid Maei, and Csaba Szepesv{\'a}ri, Shalabh Bhatnagar and Richard Sutton. Toward off-policy learning control with function approximation. In proceedings of the 27th International Conference on Machine Learning, pages 719-726, 2010.