|
![]()
Support vector machines Τμήμα Άποψης
1 #292481In machine learning, support vector machines (SVMs, also support vector networks[1]) are supervised learning models with associated learning algorithms that analyze data and recognize patterns, used for classification and regression analysis. | Support vector machineFrom Wikipedia, the free encyclopedia In machine learning, support vector machines (SVMs, also support vector networks[1]) are supervised learning models with associated learningalgorithms that analyze data and recognize patterns, used for classificationand regression analysis. The basic SVM takes a set of input data and predicts, for each given input, which of two possible classes forms the output, making it a non-probabilistic binary linear classifier. Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that assigns new examples into one category or the other. An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. New examples are then mapped into that same space and predicted to belong to a category based on which side of the gap they fall on. In addition to performing linear classification, SVMs can efficiently perform a non-linear classification using what is called the kernel trick, implicitly mapping their inputs into high-dimensional feature spaces. Contents [hide] - 1 Formal definition
- 2 History
- 3 Motivation
- 4 Linear SVM
- 4.1 Primal form
- 4.2 Dual form
- 4.3 Biased and unbiased hyperplanes
- 5 Soft margin
- 6 Nonlinear classification
- 7 Properties
- 7.1 Parameter selection
- 7.2 Issues
- 8 Extensions
- 8.1 Multiclass SVM
- 8.2 Transductive support vector machines
- 8.3 Structured SVM
- 8.4 Regression
- 9 Implementation
- 10 Applications
- 11 See also
- 12 References
- 13 External links
- 14 Bibliography
Formal definition[edit]More formally, a support vector machine constructs a hyperplane or set of hyperplanes in a high- or infinite-dimensional space, which can be used for classification, regression, or other tasks. Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the nearest training data point of any class (so-called functional margin), since in general the larger the margin the lower the generalization error of the classifier. Whereas the original problem may be stated in a finite dimensional space, it often happens that the sets to discriminate are not linearly separable in that space. For this reason, it was proposed that the original finite-dimensional space be mapped into a much higher-dimensional space, presumably making the separation easier in that space. To keep the computational load reasonable, the mappings used by SVM schemes are designed to ensure that dot products may be computed easily in terms of the variables in the original space, by defining them in terms of a kernel function  selected to suit the problem.[2] The hyperplanes in the higher-dimensional space are defined as the set of points whose dot product with a vector in that space is constant. The vectors defining the hyperplanes can be chosen to be linear combinations with parameters selected to suit the problem.[2] The hyperplanes in the higher-dimensional space are defined as the set of points whose dot product with a vector in that space is constant. The vectors defining the hyperplanes can be chosen to be linear combinations with parameters 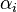 of images of feature vectors that occur in the data base. With this choice of a hyperplane, the points of images of feature vectors that occur in the data base. With this choice of a hyperplane, the points  in the feature space that are mapped into the hyperplane are defined by the relation: in the feature space that are mapped into the hyperplane are defined by the relation:  Note that if Note that if  becomes small as becomes small as  grows further away from grows further away from  , each term in the sum measures the degree of closeness of the test point , each term in the sum measures the degree of closeness of the test point  to the corresponding data base point to the corresponding data base point 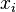 . In this way, the sum of kernels above can be used to measure the relative nearness of each test point to the data points originating in one or the other of the sets to be discriminated. Note the fact that the set of points . In this way, the sum of kernels above can be used to measure the relative nearness of each test point to the data points originating in one or the other of the sets to be discriminated. Note the fact that the set of points  mapped into any hyperplane can be quite convoluted as a result, allowing much more complex discrimination between sets which are not convex at all in the original space. mapped into any hyperplane can be quite convoluted as a result, allowing much more complex discrimination between sets which are not convex at all in the original space. History[edit]The original SVM algorithm was invented by Vladimir N. Vapnik and the current standard incarnation (soft margin) was proposed by Vapnik and Corinna Cortes in 1995.[1] Motivation[edit] H 1 does not separate the classes. H 2does, but only with a small margin. H 3separates them with the maximum margin. Classifying data is a common task in machine learning. Suppose some given data points each belong to one of two classes, and the goal is to decide which class a new data point will be in. In the case of support vector machines, a data point is viewed as a p-dimensional vector (a list of p numbers), and we want to know whether we can separate such points with a (p − 1)-dimensionalhyperplane. This is called a linear classifier. There are many hyperplanes that might classify the data. One reasonable choice as the best hyperplane is the one that represents the largest separation, or margin, between the two classes. So we choose the hyperplane so that the distance from it to the nearest data point on each side is maximized. If such a hyperplane exists, it is known as the maximum-margin hyperplane and the linear classifier it defines is known as a maximum margin classifier; or equivalently, the perceptron of optimal stability.[citation needed] Linear SVM[edit]Given some training data  , a set of n points of the form , a set of n points of the form  where the yi is either 1 or −1, indicating the class to which the point 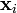 belongs. Each belongs. Each 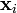 is a p-dimensional real vector. We want to find the maximum-margin hyperplane that divides the points having is a p-dimensional real vector. We want to find the maximum-margin hyperplane that divides the points having 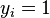 from those having from those having  . Any hyperplane can be written as the set of points . Any hyperplane can be written as the set of points  satisfying satisfying  Maximum-margin hyperplane and margins for an SVM trained with samples from two classes. Samples on the margin are called the support vectors. 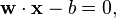 where  denotes the dot product and denotes the dot product and 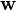 the (not necessarily normalized) normal vector to the hyperplane. The parameter the (not necessarily normalized) normal vector to the hyperplane. The parameter  determines the offset of the hyperplane from the origin along the normal vector determines the offset of the hyperplane from the origin along the normal vector 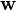 . . If the training data are linearly separable, we can select two hyperplanes in a way that they separate the data and there are no points between them, and then try to maximize their distance. The region bounded by them is called "the margin". These hyperplanes can be described by the equations  and  By using geometry, we find the distance between these two hyperplanes is 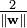 , so we want to minimize , so we want to minimize 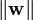 . As we also have to prevent data points from falling into the margin, we add the following constraint: for each . As we also have to prevent data points from falling into the margin, we add the following constraint: for each  either either 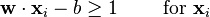 of the first class of the first class or  of the second. of the second. This can be rewritten as:  We can put this together to get the optimization problem: Minimize (in 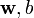 ) ) 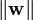 subject to (for any  ) )  Primal form[edit]The optimization problem presented in the preceding section is difficult to solve because it depends on ||w||, the norm ofw, which involves a square root. Fortunately it is possible to alter the equation by substituting ||w|| with  (the factor of 1/2 being used for mathematical convenience) without changing the solution (the minimum of the original and the modified equation have the same w and b). This is a quadratic programming optimization problem. More clearly: (the factor of 1/2 being used for mathematical convenience) without changing the solution (the minimum of the original and the modified equation have the same w and b). This is a quadratic programming optimization problem. More clearly: 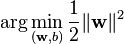 subject to (for any  ) )  By introducing Lagrange multipliers 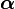 , the previous constrained problem can be expressed as , the previous constrained problem can be expressed as ![\arg\min_{\mathbf{w},b } \max_{\boldsymbol{\alpha}\geq 0 } \left\{ \frac{1}{2}\|\mathbf{w}\|^2 - \sum_{i=1}^{n}{\alpha_i[y_i(\mathbf{w}\cdot \mathbf{x_i} - b)-1]} \right\}](http://upload.wikimedia.org/math/4/9/a/49a160099f1dd1f4073081e88ef4fd0c.png) that is we look for a saddle point. In doing so all the points which can be separated as 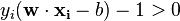 do not matter since we must set the corresponding do not matter since we must set the corresponding 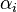 to zero. to zero. This problem can now be solved by standard quadratic programming techniques and programs. The "stationary" Karush–Kuhn–Tucker condition implies that the solution can be expressed as a linear combination of the training vectors  Only a few 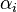 will be greater than zero. The corresponding will be greater than zero. The corresponding  are exactly the support vectors, which lie on the margin and satisfy are exactly the support vectors, which lie on the margin and satisfy  . From this one can derive that the support vectors also satisfy . From this one can derive that the support vectors also satisfy 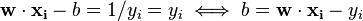 which allows one to define the offset  . In practice, it is more robust to average over all . In practice, it is more robust to average over all  support vectors: support vectors:  Dual form[edit]Writing the classification rule in its unconstrained dual form reveals that the maximum-margin hyperplane and therefore the classification task is only a function of the support vectors, the subset of the training data that lie on the margin. Using the fact that  and substituting and substituting  , one can show that the dual of the SVM reduces to the following optimization problem: , one can show that the dual of the SVM reduces to the following optimization problem: Maximize (in 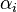 ) ) 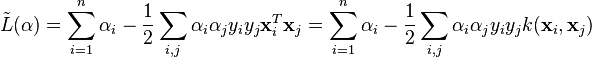 subject to (for any  ) )  and to the constraint from the minimization in   Here the kernel is defined by 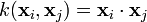 . .  can be computed thanks to the can be computed thanks to the  terms: terms:
 Biased and unbiased hyperplanes[edit]For simplicity reasons, sometimes it is required that the hyperplane pass through the origin of the coordinate system. Such hyperplanes are called unbiased, whereas general hyperplanes not necessarily passing through the origin are calledbiased. An unbiased hyperplane can be enforced by setting 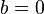 in the primal optimization problem. The corresponding dual is identical to the dual given above without the equality constraint in the primal optimization problem. The corresponding dual is identical to the dual given above without the equality constraint  Soft margin[edit]In 1995, Corinna Cortes and Vladimir N. Vapnik suggested a modified maximum margin idea that allows for mislabeled examples.[1] If there exists no hyperplane that can split the "yes" and "no" examples, the Soft Margin method will choose a hyperplane that splits the examples as cleanly as possible, while still maximizing the distance to the nearest cleanly split examples. The method introduces non-negative slack variables,  , which measure the degree of misclassification of the data , which measure the degree of misclassification of the data 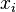  The objective function is then increased by a function which penalizes non-zero  , and the optimization becomes a trade off between a large margin and a small error penalty. If the penalty function is linear, the optimization problem becomes: , and the optimization becomes a trade off between a large margin and a small error penalty. If the penalty function is linear, the optimization problem becomes:  subject to (for any  ) ) 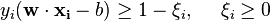 This constraint in (2) along with the objective of minimizing 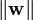 can be solved using Lagrange multipliers as done above. One has then to solve the following problem: can be solved using Lagrange multipliers as done above. One has then to solve the following problem: ![\arg\min_{\mathbf{w},\mathbf{\xi}, b } \max_{\boldsymbol{\alpha},\boldsymbol{\beta} } \left \{ \frac{1}{2}\|\mathbf{w}\|^2 +C \sum_{i=1}^n \xi_i - \sum_{i=1}^{n}{\alpha_i[y_i(\mathbf{w}\cdot \mathbf{x_i} - b) -1 + \xi_i]} - \sum_{i=1}^{n} \beta_i \xi_i \right \}](http://upload.wikimedia.org/math/8/6/4/86478542f998f3ad2d0f40a91687f8da.png) with 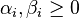 . . Dual form[edit]Maximize (in 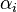 ) )  subject to (for any  ) )  and  The key advantage of a linear penalty function is that the slack variables vanish from the dual problem, with the constant Cappearing only as an additional constraint on the Lagrange multipliers. For the above formulation and its huge impact in practice, Cortes and Vapnik received the 2008 ACM Paris Kanellakis Award.[3] Nonlinear penalty functions have been used, particularly to reduce the effect of outliers on the classifier, but unless care is taken the problem becomes non-convex, and thus it is considerably more difficult to find a global solution. Nonlinear classification[edit]The original optimal hyperplane algorithm proposed by Vapnik in 1963 was alinear classifier. However, in 1992, Bernhard E. Boser, Isabelle M. Guyon andVladimir N. Vapnik suggested a way to create nonlinear classifiers by applying the kernel trick (originally proposed by Aizerman et al.[4]) to maximum-margin hyperplanes.[5] The resulting algorithm is formally similar, except that every dot product is replaced by a nonlinear kernel function. This allows the algorithm to fit the maximum-margin hyperplane in a transformed feature space. The transformation may be nonlinear and the transformed space high dimensional; thus though the classifier is a hyperplane in the high-dimensional feature space, it may be nonlinear in the original input space. If the kernel used is a Gaussian radial basis function, the corresponding feature space is a Hilbert space of infinite dimensions. Maximum margin classifiers are well regularized, so the infinite dimensions do not spoil the results. Some common kernels include: The kernel is related to the transform  by the equation by the equation 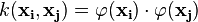 . The value w is also in the transformed space, with . The value w is also in the transformed space, with 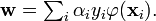 Dot products with w for classification can again be computed by the kernel trick, i.e. Dot products with w for classification can again be computed by the kernel trick, i.e.  . However, there does not in general exist a value w' such that . However, there does not in general exist a value w' such that  Properties[edit]SVMs belong to a family of generalized linear classifiers and can be interpreted as an extension of the perceptron. They can also be considered a special case of Tikhonov regularization. A special property is that they simultaneously minimize the empirical classification error and maximize the geometric margin; hence they are also known as maximum margin classifiers. A comparison of the SVM to other classifiers has been made by Meyer, Leisch and Hornik.[6] Parameter selection[edit]The effectiveness of SVM depends on the selection of kernel, the kernel's parameters, and soft margin parameter C. A common choice is a Gaussian kernel, which has a single parameter γ. The best combination of C and γ is often selected by a grid search with exponentially growing sequences of C and γ, for example,  ; ;  . Typically, each combination of parameter choices is checked using cross validation, and the parameters with best cross-validation accuracy are picked. The final model, which is used for testing and for classifying new data, is then trained on the whole training set using the selected parameters.[7] . Typically, each combination of parameter choices is checked using cross validation, and the parameters with best cross-validation accuracy are picked. The final model, which is used for testing and for classifying new data, is then trained on the whole training set using the selected parameters.[7] Potential drawbacks of the SVM are the following three aspects: - Uncalibrated class membership probabilities
- The SVM is only directly applicable for two-class tasks. Therefore, algorithms that reduce the multi-class task to several binary problems have to be applied; see the multi-class SVM section.
- Parameters of a solved model are difficult to interpret.
Extensions[edit]Multiclass SVM[edit]Multiclass SVM aims to assign labels to instances by using support vector machines, where the labels are drawn from a finite set of several elements. The dominant approach for doing so is to reduce the single multiclass problem into multiple binary classificationproblems.[8] Common methods for such reduction include:[8] [9] - Building binary classifiers which distinguish between (i) one of the labels and the rest (one-versus-all) or (ii) between every pair of classes (one-versus-one). Classification of new instances for the one-versus-all case is done by a winner-takes-all strategy, in which the classifier with the highest output function assigns the class (it is important that the output functions be calibrated to produce comparable scores). For the one-versus-one approach, classification is done by a max-wins voting strategy, in which every classifier assigns the instance to one of the two classes, then the vote for the assigned class is increased by one vote, and finally the class with the most votes determines the instance classification.
- Directed Acyclic Graph SVM (DAGSVM)[10]
- error-correcting output codes[11]
Crammer and Singer proposed a multiclass SVM method which casts the multiclass classification problem into a single optimization problem, rather than decomposing it into multiple binary classification problems.[12] See also Lee, Lin and Wahba.[13][14] Transductive support vector machines[edit]Transductive support vector machines extend SVMs in that they could also treat partially labeled data in semi-supervised learning by following the principles of transduction. Here, in addition to the training set  , the learner is also given a set , the learner is also given a set  of test examples to be classified. Formally, a transductive support vector machine is defined by the following primal optimization problem:[15] Minimize (in  ) )  subject to (for any  and any and any  ) )   and 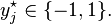 Transductive support vector machines were introduced by Vladimir N. Vapnik in 1998. Structured SVM[edit]SVMs have been generalized to structured SVMs, where the label space is structured and of possibly infinite size. Regression[edit]A version of SVM for regression was proposed in 1996 by Vladimir N. Vapnik, Harris Drucker, Christopher J. C. Burges, Linda Kaufman and Alexander J. Smola.[16] This method is called support vector regression (SVR). The model produced by support vector classification (as described above) depends only on a subset of the training data, because the cost function for building the model does not care about training points that lie beyond the margin. Analogously, the model produced by SVR depends only on a subset of the training data, because the cost function for building the model ignores any training data close to the model prediction (within a threshold  ). Another SVM version known as least squares support vector machine (LS-SVM) has been proposed by Suykens and Vandewalle.[17] ). Another SVM version known as least squares support vector machine (LS-SVM) has been proposed by Suykens and Vandewalle.[17] Implementation[edit]The parameters of the maximum-margin hyperplane are derived by solving the optimization. There exist several specialized algorithms for quickly solving the QP problem that arises from SVMs, mostly relying on heuristics for breaking the problem down into smaller, more-manageable chunks. A common method is Platt's Sequential Minimal Optimization (SMO) algorithm, which breaks the problem down into 2-dimensional sub-problems that may be solved analytically, eliminating the need for a numerical optimization algorithm. Another approach is to use an interior point method that uses Newton-like iterations to find a solution of the Karush–Kuhn–Tucker conditions of the primal and dual problems.[18] Instead of solving a sequence of broken down problems, this approach directly solves the problem as a whole. To avoid solving a linear system involving the large kernel matrix, a low rank approximation to the matrix is often used in the kernel trick. Applications[edit]SVMs can be used to solve various real world problems: - SVMs are helpful in text and hypertext categorization as their application can significantly reduce the need for labeled training instances in both the standard inductive and transductive settings.
- Classification of images can also be performed using SVMs. Experimental results show that SVMs achieve significantly higher search accuracy than traditional query refinement schemes after just three to four rounds of relevance feedback.
- SVMs are also useful in medical science to classify proteins with up to 90% of the compounds classified correctly.
- Hand-written characters can be recognized using SVM
See also[edit]References[edit] - ^ Jump up to:a b c Cortes, Corinna; and Vapnik, Vladimir N.; "Support-Vector Networks", Machine Learning, 20, 1995.http://www.springerlink.com/content/k238jx04hm87j80g/
- Jump up^ *Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, B. P. (2007). "Section 16.5. Support Vector Machines". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press.ISBN 978-0-521-88068-8.
- Jump up^ ACM Website, Press release of March 17th 2009. http://www.acm.org/press-room/news-releases/awards-08-groupa
- Jump up^ Aizerman, Mark A.; Braverman, Emmanuel M.; and Rozonoer, Lev I. (1964). "Theoretical foundations of the potential function method in pattern recognition learning". Automation and Remote Control 25: 821–837.
- Jump up^ Boser, Bernhard E.; Guyon, Isabelle M.; and Vapnik, Vladimir N.; A training algorithm for optimal margin classifiers. In Haussler, David (editor); 5th Annual ACM Workshop on COLT, pages 144–152, Pittsburgh, PA, 1992. ACM Press
- Jump up^ Meyer, David; Leisch, Friedrich; and Hornik, Kurt; The support vector machine under test, Neurocomputing 55(1–2): 169–186, 2003 http://dx.doi.org/10.1016/S0925-2312(03)00431-4
- Jump up^ Hsu, Chih-Wei; Chang, Chih-Chung; and Lin, Chih-Jen (2003). A Practical Guide to Support Vector Classification(Technical report). Department of Computer Science and Information Engineering, National Taiwan University.
- ^ Jump up to:a b Duan, Kai-Bo; and Keerthi, S. Sathiya (2005). "Which Is the Best Multiclass SVM Method? An Empirical Study".Proceedings of the Sixth International Workshop on Multiple Classifier Systems. Lecture Notes in Computer Science 3541: 278. doi:10.1007/11494683_28. ISBN 978-3-540-26306-7.
- Jump up^ Hsu, Chih-Wei; and Lin, Chih-Jen (2002). "A Comparison of Methods for Multiclass Support Vector Machines". IEEE Transactions on Neural Networks.
- Jump up^ Platt, John; Cristianini, N.; and Shawe-Taylor, J. (2000). "Large margin DAGs for multiclass classification". In Solla, Sara A.; Leen, Todd K.; and Müller, Klaus-Robert; eds. Advances in Neural Information Processing Systems. MIT Press. pp. 547–553.
- Jump up^ Dietterich, Thomas G.; and Bakiri, Ghulum; Bakiri (1995). "Solving Multiclass Learning Problems via Error-Correcting Output Codes". Journal of Artificial Intelligence Research, Vol. 2 2: 263–286. arXiv:cs/9501101.Bibcode:1995cs........1101D.
- Jump up^ Crammer, Koby; and Singer, Yoram (2001). "On the Algorithmic Implementation of Multiclass Kernel-based Vector Machines". J. of Machine Learning Research 2: 265–292.
- Jump up^ Lee, Y.; Lin, Y.; and Wahba, G. (2001). "Multicategory Support Vector Machines". Computing Science and Statistics 33.
- Jump up^ Lee, Y.; Lin, Y.; and Wahba, G. (2004). "Multicategory Support Vector Machines, Theory, and Application to the Classification of Microarray Data and Satellite Radiance Data". Journal of the American Statistical Association 99 (465): 67–81. doi:10.1198/016214504000000098.
- Jump up^ Joachims, Thorsten; "Transductive Inference for Text Classification using Support Vector Machines", Proceedings of the 1999 International Conference on Machine Learning (ICML 1999), pp. 200-209.
- Jump up^ Drucker, Harris; Burges, Christopher J. C.; Kaufman, Linda; Smola, Alexander J.; and Vapnik, Vladimir N. (1997); "Support Vector Regression Machines", in Advances in Neural Information Processing Systems 9, NIPS 1996, 155–161, MIT Press.
- Jump up^ Suykens, Johan A. K.; Vandewalle, Joos P. L.; Least squares support vector machine classifiers, Neural Processing Letters, vol. 9, no. 3, Jun. 1999, pp. 293–300.
- Jump up^ Ferris, Michael C.; and Munson, Todd S. (2002). "Interior-point methods for massive support vector machines". SIAM Journal on Optimization 13 (3): 783–804. doi:10.1137/S1052623400374379.
External links[edit] - Burges, Christopher J. C.; A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery 2:121–167, 1998
- www.kernel-machines.org (general information and collection of research papers)
- Teknomo, K. SVM tutorial using spreadsheet Visual Introduction to SVM.
- www.support-vector-machines.org (Literature, Review, Software, Links related to Support Vector Machines — Academic Site)
- videolectures.net (SVM-related video lectures)
- Animation clip: SVM with polynomial kernel visualization
- Fletcher, Tristan; A very basic SVM tutorial for complete beginners
- Karatzoglou, Alexandros et al.; Support Vector Machines in R, Journal of Statistical Software April 2006, Volume 15, Issue 9.
- Vlasveld, Roemer; Introduction to one-class SVMs
- Shogun (toolbox) contains about 20 different implementations of SVMs, written in C++ with MATLAB, Octave, Python, R, Java, Lua, Ruby and C# interfaces
- libsvm LIBSVM is a popular library of SVM learners
- liblinear liblinear is a library for large linear classification including some SVMs
- flssvm flssvm is a least squares svm implementation written in fortran
- Shark Shark is a C++ machine learning library implementing various types of SVMs
- dlib dlib is a C++ library for working with kernel methods and SVMs
- SVM light is a collection of software tools for learning and classification using SVM.
- SVMJS live demo is a GUI demo for Javascript implementation of SVMs
- Stanford University Andrew Ng Video on SVM
- Byvatov E, Schneider G., Support vector machine applications in bioinformatics.Appl Bioinformatics. 2003;2(2):67-77.
- Simon Tong,Edward Chang, Support vector machine active learning for image retrieval, Proceeding MULTIMEDIA '01 Proceedings of the ninth ACM international conference on Multimedia Pages 107-118
- Simon Tong , Daphne Koller,Support Vector Machine Active Learning with Applications to Text Classification ,JOURNAL OF MACHINE LEARNING RESEARCH (2001)
Bibliography[edit] - Theodoridis, Sergios; and Koutroumbas, Konstantinos; "Pattern Recognition", 4th Edition, Academic Press, 2009,ISBN 978-1-59749-272-0
- Cristianini, Nello; and Shawe-Taylor, John; An Introduction to Support Vector Machines and other kernel-based learning methods, Cambridge University Press, 2000. ISBN 0-521-78019-5 ([1] SVM Book)
- Huang, Te-Ming; Kecman, Vojislav; and Kopriva, Ivica (2006); Kernel Based Algorithms for Mining Huge Data Sets, inSupervised, Semi-supervised, and Unsupervised Learning, Springer-Verlag, Berlin, Heidelberg, 260 pp. 96 illus., Hardcover, ISBN 3-540-31681-7 [2]
- Kecman, Vojislav; Learning and Soft Computing — Support Vector Machines, Neural Networks, Fuzzy Logic Systems, The MIT Press, Cambridge, MA, 2001.[3]
- Schölkopf, Bernhard; and Smola, Alexander J.; Learning with Kernels, MIT Press, Cambridge, MA, 2002. ISBN 0-262-19475-9
- Schölkopf, Bernhard; Burges, Christopher J. C.; and Smola, Alexander J. (editors); Advances in Kernel Methods: Support Vector Learning, MIT Press, Cambridge, MA, 1999. ISBN 0-262-19416-3. [4]
- Shawe-Taylor, John; and Cristianini, Nello; Kernel Methods for Pattern Analysis, Cambridge University Press, 2004.ISBN 0-521-81397-2 ([5] Kernel Methods Book)
- Steinwart, Ingo; and Christmann, Andreas; Support Vector Machines, Springer-Verlag, New York, 2008. ISBN 978-0-387-77241-7 ([6] SVM Book)
- Tan, Peter Jing; and Dowe, David L. (2004); MML Inference of Oblique Decision Trees, Lecture Notes in Artificial Intelligence (LNAI) 3339, Springer-Verlag, pp1082-1088. (This paper uses minimum message length (MML) and actually incorporates probabilistic support vector machines in the leaves of decision trees.)
- Vapnik, Vladimir N.; The Nature of Statistical Learning Theory, Springer-Verlag, 1995. ISBN 0-387-98780-0
- Vapnik, Vladimir N.; and Kotz, Samuel; Estimation of Dependences Based on Empirical Data, Springer, 2006. ISBN 0-387-30865-2, 510 pages [this is a reprint of Vapnik's early book describing philosophy behind SVM approach. The 2006 Appendix describes recent development].
- Fradkin, Dmitriy; and Muchnik, Ilya; Support Vector Machines for Classification in Abello, J.; and Carmode, G. (Eds);Discrete Methods in Epidemiology, DIMACS Series in Discrete Mathematics and Theoretical Computer Science, volume 70, pp. 13–20, 2006. [7]. Succinctly describes theoretical ideas behind SVM.
- Bennett, Kristin P.; and Campbell, Colin; Support Vector Machines: Hype or Hallelujah?, SIGKDD Explorations, 2, 2, 2000, 1–13. [8]. Excellent introduction to SVMs with helpful figures.
- Ivanciuc, Ovidiu; Applications of Support Vector Machines in Chemistry, in Reviews in Computational Chemistry, Volume 23, 2007, pp. 291–400. Reprint available: [9]
- Catanzaro, Bryan; Sundaram, Narayanan; and Keutzer, Kurt; Fast Support Vector Machine Training and Classification on Graphics Processors, in International Conference on Machine Learning, 2008 [10]
- Campbell, Colin; and Ying, Yiming; Learning with Support Vector Machines, 2011, Morgan and Claypool. ISBN 978-1-60845-616-1. [11]
|
+Αναφορές (1) - ΑναφορέςΠροσθήκη αναφοράςList by: CiterankMapLink[1] Wikipedia
Συγγραφέας: Various
Παρατέθηκε από: Roger Yau 2:37 PM 21 October 2013 GMT
Citerank: (28) 291862AODE - Averaged one-dependence estimatorsAveraged one-dependence estimators (AODE) is a probabilistic classification learning technique. It was developed to address the attribute-independence problem of the popular naive Bayes classifier. It frequently develops substantially more accurate classifiers than naive Bayes at the cost of a modest increase in the amount of computation.109FDEF6, 291863Artificial neural networkIn computer science and related fields, artificial neural networks are computational models inspired by animal central nervous systems (in particular the brain) that are capable of machine learning and pattern recognition. They are usually presented as systems of interconnected "neurons" that can compute values from inputs by feeding information through the network.109FDEF6, 291936BackpropagationBackpropagation, an abbreviation for "backward propagation of errors", is a common method of training artificial neural networks. From a desired output, the network learns from many inputs, similar to the way a child learns to identify a dog from examples of dogs.109FDEF6, 291937Bayesian statisticsBayesian statistics is a subset of the field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities. Such an interpretation is only one of a number of interpretations of probability and there are other statistical techniques that are not based on "degrees of belief".109FDEF6, 291938Naive Bayes classifierA naive Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem with strong (naive) independence assumptions. A more descriptive term for the underlying probability model would be "independent feature model". An overview of statistical classifiers is given in the article on Pattern recognition.109FDEF6, 291939Bayesian networkA Bayesian network, Bayes network, belief network, Bayes(ian) model or probabilistic directed acyclic graphical model is a probabilistic graphical model (a type of statistical model) that represents a set of random variables and their conditional dependencies via a directed acyclic graph (DAG). For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. 109FDEF6, 291941Case-based reasoningCase-based reasoning (CBR), broadly construed, is the process of solving new problems based on the solutions of similar past problems. An auto mechanic who fixes an engine by recalling another car that exhibited similar symptoms is using case-based reasoning. So, too, an engineer copying working elements of nature (practicing biomimicry), is treating nature as a database of solutions to problems. Case-based reasoning is a prominent kind of analogy making.109FDEF6, 291942Decision tree learningDecision tree learning uses a decision tree as a predictive model which maps observations about an item to conclusions about the item's target value. It is one of the predictive modelling approaches used in statistics, data mining and machine learning. More descriptive names for such tree models are classification trees or regression trees. In these tree structures, leaves represent class labels and branches represent conjunctions of features that lead to those class labels.109FDEF6, 291943Inductive logic programmingInductive logic programming (ILP) is a subfield of machine learning which uses logic programming as a uniform representation for examples, background knowledge and hypotheses. Given an encoding of the known background knowledge and a set of examples represented as a logical database of facts, an ILP system will derive a hypothesised logic program which entails all the positive and none of the negative examples.109FDEF6, 291944Gaussian process regression (Kriging)Kriging is a method to build an approximation of a function from a set of evaluations of the function at a finite set of points. The method originates from the domain of geostatistics and is now widely used in the domain of spatial analysis and computer experiments. The technique is also known as Gaussian process regression, Kolmogorov Wiener prediction, or Best Linear Unbiased Prediction.109FDEF6, 291945Gene expression programmingGene expression programming (GEP) is an evolutionary algorithm that creates computer programs or models. These computer programs are complex tree structures that learn and adapt by changing their sizes, shapes, and composition, much like a living organism. And like living organisms, the computer programs of GEP are also encoded in simple linear chromosomes of fixed length. Thus, GEP is a genotype-phenotype system.109FDEF6, 291946Group method of data handlingGroup method of data handling (GMDH) is a family of inductive algorithms for computer-based mathematical modeling of multi-parametric datasets that features fully automatic structural and parametric optimization of models.109FDEF6, 291947Learning automataA branch of the theory of adaptive control is devoted to learning automata surveyed by Narendra and Thathachar which were originally described explicitly as finite state automata. Learning automata select their current action based on past experiences from the environment.109FDEF6, 291948Supervised learningSupervised learning is the machine learning task of inferring a function from labeled training data.[1] The training data consist of a set of training examples. In supervised learning, each example is a pair consisting of an input object (typically a vector) and a desired output value (also called the supervisory signal). A supervised learning algorithm analyzes the training data and produces an inferred function, which can be used for mapping new examples. 25CBCBFF, 291950Unsupervised learningIn machine learning, the problem of unsupervised learning is that of trying to find hidden structure in unlabeled data. Since the examples given to the learner are unlabeled, there is no error or reward signal to evaluate a potential solution. This distinguishes unsupervised learning from supervised learning and reinforcement learning.25CBCBFF, 291951Reinforcement learningReinforcement learning is an area of machine learning inspired by behaviorist psychology, concerned with how software agents ought to take actions in an environment so as to maximize some notion of cumulative reward. The problem, due to its generality, is studied in many other disciplines, such as game theory, control theory, operations research, information theory, simulation-based optimization, statistics, and genetic algorithms.25CBCBFF, 292450Hierarchical clusteringIn data mining, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:
Agglomerative: This is a "bottom up" approach: each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy.
Divisive: This is a "top down" approach: all observations start in one cluster, and splits are performed recursively as one moves down the hierarch109FDEF6, 292451Association rule learningAssociation rule learning is a popular and well researched method for discovering interesting relations between variables in large databases. It is intended to identify strong rules discovered in databases using different measures of interestingness.109FDEF6, 292454Others25CBCBFF, 292455Learning Vector QuantizationIn computer science, Learning Vector Quantization (LVQ), is a prototype-based supervised classification algorithm. LVQ is the supervised counterpart of vector quantization systems.
LVQ can be understood as a special case of an artificial neural network, more precisely, it applies a winner-take-all Hebbian learning-based approach. It is a precursor to Self-organizing maps (SOM) and related to Neural gas, and to the k-Nearest Neighbor algorithm (k-NN). LVQ was invented by Teuvo Kohonen.109FDEF6, 292463Logistic Model TreeLMT is a classification model with an associated supervised training algorithm that combines logistic regression (LR) and decision tree learning. Logistic model trees are based on the earlier idea of a model tree: a decision tree that has linear regression models at its leaves to provide a piecewise linear regression model (where ordinary decision trees with constants at their leaves would produce a piecewise constant model).109FDEF6, 292464Minimum message lengthMinimum message length (MML) is a formal information theory restatement of Occam's Razor: even when models are not equal in goodness of fit accuracy to the observed data, the one generating the shortest overall message is more likely to be correct (where the message consists of a statement of the model, followed by a statement of data encoded concisely using that model). MML was invented by Chris Wallace, first appearing in the seminal (Wallace and Boulton, 1968).109FDEF6, 292465Lazy learningIn artificial intelligence, lazy learning is a learning method in which generalization beyond the training data is delayed until a query is made to the system, as opposed to in eager learning, where the system tries to generalize the training data before receiving queries.109FDEF6, 292466Instance-based learninginstance-based learning or memory-based learning is a family of learning algorithms that, instead of performing explicit generalization, compare new problem instances with instances seen in training, which have been stored in memory. Instance-based learning is a kind of lazy learning.109FDEF6, 292475k-nearest neighbor algorithmIn pattern recognition, the k-nearest neighbor algorithm (k-NN) is a non-parametric method for classifying objects based on closest training examples in the feature space. k-NN is a type of instance-based learning, or lazy learning where the function is only approximated locally and all computation is deferred until classification. 109FDEF6, 292476Analogical modelingAnalogical modeling (hereafter AM) is a formal theory of exemplar-based analogical reasoning, proposed by Royal Skousen, professor of Linguistics and English language at Brigham Young University in Provo, Utah. It is applicable to language modeling and other categorization tasks. Analogical modeling is related to connectionism and nearest neighbor approaches, in that it is data-based rather than abstraction-based.109FDEF6, 292478Probably approximately correct learningIn this framework, the learner receives samples and must select a generalization function (called the hypothesis) from a certain class of possible functions. The goal is that, with high probability (the "probably" part), the selected function will have low generalization error (the "approximately correct" part). The learner must be able to learn the concept given any arbitrary approximation ratio, probability of success, or distribution of the samples.109FDEF6, 292480Ripple-down rulesRipple Down Rules is a way of approaching knowledge acquisition. Knowledge acquisition refers to the transfer of knowledge from human experts to knowledge based systems.109FDEF6 URL: |
|
|