|
![]()
| Analogical modeling Composant1 #292476 Analogical modeling (hereafter AM) is a formal theory of exemplar-based analogical reasoning, proposed by Royal Skousen, professor of Linguistics and English language at Brigham Young University in Provo, Utah. It is applicable to language modeling and other categorization tasks. Analogical modeling is related to connectionism and nearest neighbor approaches, in that it is data-based rather than abstraction-based. | Analogical modeling (hereafter AM) is a formal theory of exemplar-based analogical reasoning, proposed by Royal Skousen, professor of Linguistics and English language at Brigham Young University in Provo, Utah. It is applicable to language modeling and other categorization tasks. Analogical modeling is related to connectionism and nearest neighbor approaches, in that it is data-based rather than abstraction-based; but it is distinguished by its ability to cope with imperfect datasets (such as caused by simulated short term memory limits) and to base predictions on all relevant segments of the dataset, whether near or far. In language modeling, AM has successfully predicted empirically valid forms for which no theoretical explanation was known (see the discussion of Finnish morphology in Skousen et al. 2002). Implementation of the model[edit]Overview[edit]An exemplar-based model consists of a general-purpose modeling engine and a problem-specific dataset. Within the dataset, each exemplar (a case to be reasoned from, or an informative past experience) appears as a feature vector: a row of values for parameters that describe the problem. For example, in a spelling-to-sound task, the feature vector might consist of the letters of a word. Each exemplar in the dataset is stored with an outcome, such as a phoneme or phone to be generated. When the model is presented with a novel situation (in the form of an outcome-less feature vector), the engine algorithmically sorts the dataset to find exemplars that helpfully resemble it, and selects one, whose outcome is the model's prediction. The particulars of this algorithm distinguish one exemplar-based modeling system from another. In AM, we think of the feature values as characterizing a context, and the outcome as a behavior that occurs within that context. Accordingly, the novel situation is known as the given context. Given the known features of the context, the AM engine systematically generates all contexts that include it (all of its supracontexts), and extracts from the dataset the exemplars that belong to each. The engine then discards those supracontexts whose outcomes are inconsistent (this measure of consistency will be discussed further below), leaving an analogical set of supracontexts, and probabilistically selects an exemplar from the analogical set with a bias toward those in large supracontexts. This multilevel search exponentially magnifies the likelihood of a behavior's being predicted as it occurs reliably in settings that specifically resemble the given context. Analogical modeling in detail[edit]AM performs the same process for each case it is asked to evaluate. The given context, consisting of n variables, is used as a template to generate two-to-the-n supracontexts. Each supracontext is a set of exemplars in which one or more variables have the same values that they do in the given context, and the other variables are ignored. In effect, each is a view of the data, created by filtering for some criteria of similarity to the given context, and the total set of supracontexts exhausts all such views. Alternatively, each supracontext is a theory of the task or a proposed rule whose predictive power needs to be evaluated. It is important to note that the supracontexts are not equal peers one with another; they are arranged by their distance from the given context, forming a hierarchy. If a supracontext specifies all of the variables that another one does and more, it is a subcontext of that other one, and it lies closer to the given context. (The hierarchy is not strictly branching; each supracontext can itself be a subcontext of several others, and can have several subcontexts.) This hierarchy becomes significant in the next step of the algorithm. The engine now chooses the analogical set from among the supracontexts. A supracontext may contain exemplars that only exhibit one behavior; it is deterministically homogeneous and is included. It is a view of the data that displays regularity, or a relevant theory that has never yet been disproven. A supracontext may exhibit several behaviors, but contain no exemplars that occur in any more specific supracontext (that is, in any of its subcontexts); in this case it is non-deterministically homogeneous and is included. Here there is no great evidence that a systematic behavior occurs, but also no counterargument. Finally, a supracontext may be heterogeneous, meaning that it exhibits behaviors that are found in a subcontext (closer to the given context), and also behaviors that are not. Where the ambiguous behavior of the nondeterministically homogeneous supracontext was accepted, this is rejected because the intervening subcontext demonstrates that there is a better theory to be found. The heterogeneous supracontext is therefore excluded. This guarantees that we see an increase in meaningfully consistent behavior in the analogical set as we approach the given context. With the analogical set chosen, each appearance of an exemplar (for a given exemplar may appear in several of the analogical supracontexts) is given a pointer to every other appearance of an exemplar within its supracontexts. One of these pointers is then selected at random and followed, and the exemplar to which it points provides the outcome. This gives each supracontext an importance proportional to the square of its size, and makes each exemplar likely to be selected in direct proportion to the sum of the sizes of all analogically consistent supracontexts in which it appears. Then, of course, the probability of predicting a particular outcome is proportional to the summed probabilities of all the exemplars that support it. (Skousen 2002, in Skousen et al. 2002, pp. 11–25, and Skousen 2003, both passim) Formulas[edit]Given a context with  elements: elements: - total number of pairings:
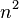 - number of agreements for outcome i:
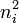 - number of disagreements for outcome i:
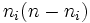 - total number of agreements:
 - total number of disagreements:
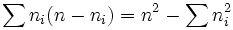 Example[edit]This terminology is best understood through an example. In the example used in the second chapter of Skousen (1989), each context consists of three variables with potential values 0-3 - Variable 1: 0,1,2,3
- Variable 2: 0,1,2,3
- Variable 3: 0,1,2,3
The two outcomes for the dataset are e and r, and the exemplars are: 3 1 0 e 0 3 2 r 2 1 0 r 2 1 2 r 3 1 1 r We define a network of pointers like so: 
The solid lines represent pointers between exemplars with matching outcomes; the dotted lines represent pointers between exemplars with non-matching outcomes. The statistics for this example are as follows:  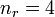 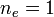 - total number of pairings:
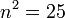 - number of agreements for outcome r:
 - number of agreements for outcome e:
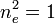 - number of disagreements for outcome r:
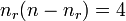 - number of disagreements for outcome e:
 - total number of agreements:
 - total number of disagreements:
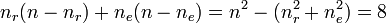 - uncertainty or fraction of disagreement:
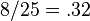 Behavior can only be predicted for a given context; in this example, let us predict the outcome for the context "3 1 2". To do this, we first find all of the contexts containing the given context; these contexts are called supracontexts. We find the supracontexts by systematically eliminating the variables in the given context; with m variables, there will generally be 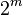 supracontexts. The following table lists each of the sub- and supracontexts; x means "not x", and - means "anything". supracontexts. The following table lists each of the sub- and supracontexts; x means "not x", and - means "anything". | Supracontext | Subcontexts | | 3 1 2 | 3 1 2 | | 3 1 - | 3 1 2, 3 1 2 | | 3 - 2 | 3 1 2, 3 1 2 | | - 1 2 | 3 1 2, 3 1 2 | | 3 - - | 3 1 2, 3 1 2, 3 1 2, 3 1 2 | | - 1 - | 3 1 2, 3 1 2, 3 1 2, 3 1 2 | | - - 2 | 3 1 2, 3 1 2, 3 1 2, 3 1 2 | | - - - | 3 1 2, 3 1 2, 3 1 2, 3 1 2, 3 1 2, 3 1 2, 3 1 2, 3 1 2 | These contexts are shown in the venn diagram below: 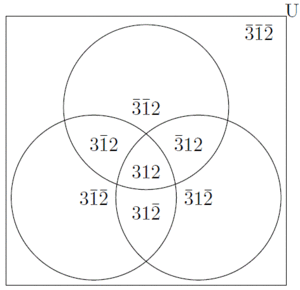
The next step is to determine which exemplars belong to which contexts in order to determine which of the contexts are homogeneous. The table below shows each of the subcontexts, their behavior in terms of the given exemplars, and the number of disagreements within the behavior: | Subcontext | Behavior | Disagreements | | 3 1 2 | (empty) | 0 | | 3 1 2 | 3 1 0 e, 3 1 1 r | 2 | | 3 1 2 | (empty) | 0 | | 3 1 2 | 2 1 2 r | 0 | | 3 1 2 | (empty) | 0 | | 3 1 2 | 2 1 0 r | 0 | | 3 1 2 | 0 3 2 r | 0 | | 31 2 | (empty) | 0 | Analyzing the subcontexts in the table above, we see that there is only 1 subcontext with any disagreements: "3 1 2", which in the dataset consists of "3 1 0 e" and "3 1 1 r". There are 2 disagreements in this subcontext; 1 pointing from each of the exemplars to the other (see the pointer network pictured above). Therefore, only supracontexts containing this subcontext will contain any disagreements. We use a simple rule to identify the homogeneous supracontexts: If the number if disagreements in the supracontext is greater than the number of disagreements in the contained subcontext, we say that it is heterogeneous; otherwise, it is homogeneous.
There are 3 situations that produce a homogeneous supracontext: - The supracontext is empty. This is the case for "3 - 2", which contains no data points. There can be no increase in the number of disagreements, and the supracontext is trivially homogeneous.
- The supracontext is deterministic, meaning that only one type of outcome occurs in it. This is the case for "- 1 2" and "- - 2", which contain only data with the r outcome.
- Only one subcontext contains any data. The subcontext does not have to be deterministic for the supracontext to be homogeneous. For example, while the supracontexts "3 1 -" and "- 1 2" are deterministic and only contain one non-empty subcontext, "3 - -" contains only the subcontext "3 1 2". This subcontext contains "3 1 0 e" and "3 1 1 r", making it non-deterministic. We say that this type of supracontext is unobstructed and non-deterministic.
The only two heterogeneous supracontexts are "- 1 -" and "- - -". In both of them, it is the combination of the non-deterministic "3 1 2" with other subcontexts containing the r outcome which causes the heterogeneity. There is actually a 4th type of homogeneous supracontext: it contains more than one non-empty subcontext and it is non-deterministic, but the frequency of outcomes in each sub-context is exactly the same. Analogical modeling does not consider this situation, however, for 2 reasons: - Determining whether this 4 situation has occurred requires a
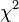 test. This is the only test of homogeneity that requires arithmetic, and ignoring it allows our tests of homogeneity to become statistically free, which makes AM better for modeling human reasoning. test. This is the only test of homogeneity that requires arithmetic, and ignoring it allows our tests of homogeneity to become statistically free, which makes AM better for modeling human reasoning. - It is an extremely rare situation, and thus ignoring it will can be expected not to have a large effect on the predicted outcome.
Next we construct the analogical set, which consists of all of the pointers and outcomes from the homogeneous supracontexts. The figure below shows the pointer network with the homogeneous contexts highlighted. 
The pointers are summarized in the following table: Homogeneous
supracontext | Occurrences | Number of
pointers | | | | | 3 1 - | "3 1 0 e", "3 1 1 r" | | | - 1 2 | "2 1 2 r" | | | 3 - - | "3 1 0 e", "3 1 1 r" | | | - - 2 | "2 1 2 r", "0 3 2 r" | | | Totals: | | 4 of the pointers in the analogical set are associated with the outcome e, and the other 9 are associated with r. In AM, a pointer is randomly selected and the outcome it points to is predicted. With a total of 13 pointers, the probability of the outcome e being predicted is 4/13 or 30.8%, and for outcome r it is 9/13 or 69.2%. We can create a more detailed account by listing the pointers for each of the occurrences in the homogeneous supracontexts: | Occurrence | Number of
homogeneous
supracontexts | Number of
pointers | Analogical
effect | | 3 1 0 e | 2 | 4 | 30.8% | | 3 1 1 r | 2 | 4 | 30.8% | | 2 1 2 r | 2 | 3 | 23.1% | | 0 3 2 r | 1 | 2 | 15.4% | | 2 1 0 r | 0 | 0 | 0.0% | We can then see the analogical effect of each of the instances in the data set. Historical Context[edit]Analogy has been considered useful in describing language at least since the time of Saussure. Noam Chomsky and others have more recently criticized analogy as too vague to really be useful (Bańko 1991), an appeal to a deus ex machina. Skousen's proposal appears to address that criticism by proposing an explicit mechanism for analogy, which can be tested for psychological validity. Applications[edit]Analogical modeling has been employed in experiments ranging from phonology and morphology (linguistics) to orthography and syntax. Problems[edit]Though analogical modeling aims to create a model free from rules seen as contrived by linguists, in its current form it still requires researchers to select which variables to take into consideration. This is necessary because of the so-called "exponential explosion" of processing power requirements of the computer software used to implement analogical modeling. Recent research suggests that quantum computing could provide the solution to such performance bottlenecks (Skousen et al. 2002, see pp 45–47). See also[edit]References[edit]External links[edit] |
+Citations (1) - CitationsAjouter une citationList by: CiterankMapLink[1] Wikipedia
En citant: Various
Cité par: Roger Yau 2:29 PM 21 October 2013 GMT
Citerank: (28) 291862AODE - Averaged one-dependence estimatorsAveraged one-dependence estimators (AODE) is a probabilistic classification learning technique. It was developed to address the attribute-independence problem of the popular naive Bayes classifier. It frequently develops substantially more accurate classifiers than naive Bayes at the cost of a modest increase in the amount of computation.109FDEF6, 291863Artificial neural networkIn computer science and related fields, artificial neural networks are computational models inspired by animal central nervous systems (in particular the brain) that are capable of machine learning and pattern recognition. They are usually presented as systems of interconnected "neurons" that can compute values from inputs by feeding information through the network.109FDEF6, 291936BackpropagationBackpropagation, an abbreviation for "backward propagation of errors", is a common method of training artificial neural networks. From a desired output, the network learns from many inputs, similar to the way a child learns to identify a dog from examples of dogs.109FDEF6, 291937Bayesian statisticsBayesian statistics is a subset of the field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities. Such an interpretation is only one of a number of interpretations of probability and there are other statistical techniques that are not based on "degrees of belief".109FDEF6, 291938Naive Bayes classifierA naive Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem with strong (naive) independence assumptions. A more descriptive term for the underlying probability model would be "independent feature model". An overview of statistical classifiers is given in the article on Pattern recognition.109FDEF6, 291939Bayesian networkA Bayesian network, Bayes network, belief network, Bayes(ian) model or probabilistic directed acyclic graphical model is a probabilistic graphical model (a type of statistical model) that represents a set of random variables and their conditional dependencies via a directed acyclic graph (DAG). For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. 109FDEF6, 291941Case-based reasoningCase-based reasoning (CBR), broadly construed, is the process of solving new problems based on the solutions of similar past problems. An auto mechanic who fixes an engine by recalling another car that exhibited similar symptoms is using case-based reasoning. So, too, an engineer copying working elements of nature (practicing biomimicry), is treating nature as a database of solutions to problems. Case-based reasoning is a prominent kind of analogy making.109FDEF6, 291942Decision tree learningDecision tree learning uses a decision tree as a predictive model which maps observations about an item to conclusions about the item's target value. It is one of the predictive modelling approaches used in statistics, data mining and machine learning. More descriptive names for such tree models are classification trees or regression trees. In these tree structures, leaves represent class labels and branches represent conjunctions of features that lead to those class labels.109FDEF6, 291943Inductive logic programmingInductive logic programming (ILP) is a subfield of machine learning which uses logic programming as a uniform representation for examples, background knowledge and hypotheses. Given an encoding of the known background knowledge and a set of examples represented as a logical database of facts, an ILP system will derive a hypothesised logic program which entails all the positive and none of the negative examples.109FDEF6, 291944Gaussian process regression (Kriging)Kriging is a method to build an approximation of a function from a set of evaluations of the function at a finite set of points. The method originates from the domain of geostatistics and is now widely used in the domain of spatial analysis and computer experiments. The technique is also known as Gaussian process regression, Kolmogorov Wiener prediction, or Best Linear Unbiased Prediction.109FDEF6, 291945Gene expression programmingGene expression programming (GEP) is an evolutionary algorithm that creates computer programs or models. These computer programs are complex tree structures that learn and adapt by changing their sizes, shapes, and composition, much like a living organism. And like living organisms, the computer programs of GEP are also encoded in simple linear chromosomes of fixed length. Thus, GEP is a genotype-phenotype system.109FDEF6, 291946Group method of data handlingGroup method of data handling (GMDH) is a family of inductive algorithms for computer-based mathematical modeling of multi-parametric datasets that features fully automatic structural and parametric optimization of models.109FDEF6, 291947Learning automataA branch of the theory of adaptive control is devoted to learning automata surveyed by Narendra and Thathachar which were originally described explicitly as finite state automata. Learning automata select their current action based on past experiences from the environment.109FDEF6, 291948Supervised learningSupervised learning is the machine learning task of inferring a function from labeled training data.[1] The training data consist of a set of training examples. In supervised learning, each example is a pair consisting of an input object (typically a vector) and a desired output value (also called the supervisory signal). A supervised learning algorithm analyzes the training data and produces an inferred function, which can be used for mapping new examples. 25CBCBFF, 291950Unsupervised learningIn machine learning, the problem of unsupervised learning is that of trying to find hidden structure in unlabeled data. Since the examples given to the learner are unlabeled, there is no error or reward signal to evaluate a potential solution. This distinguishes unsupervised learning from supervised learning and reinforcement learning.25CBCBFF, 291951Reinforcement learningReinforcement learning is an area of machine learning inspired by behaviorist psychology, concerned with how software agents ought to take actions in an environment so as to maximize some notion of cumulative reward. The problem, due to its generality, is studied in many other disciplines, such as game theory, control theory, operations research, information theory, simulation-based optimization, statistics, and genetic algorithms.25CBCBFF, 292450Hierarchical clusteringIn data mining, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:
Agglomerative: This is a "bottom up" approach: each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy.
Divisive: This is a "top down" approach: all observations start in one cluster, and splits are performed recursively as one moves down the hierarch109FDEF6, 292451Association rule learningAssociation rule learning is a popular and well researched method for discovering interesting relations between variables in large databases. It is intended to identify strong rules discovered in databases using different measures of interestingness.109FDEF6, 292454Others25CBCBFF, 292455Learning Vector QuantizationIn computer science, Learning Vector Quantization (LVQ), is a prototype-based supervised classification algorithm. LVQ is the supervised counterpart of vector quantization systems.
LVQ can be understood as a special case of an artificial neural network, more precisely, it applies a winner-take-all Hebbian learning-based approach. It is a precursor to Self-organizing maps (SOM) and related to Neural gas, and to the k-Nearest Neighbor algorithm (k-NN). LVQ was invented by Teuvo Kohonen.109FDEF6, 292463Logistic Model TreeLMT is a classification model with an associated supervised training algorithm that combines logistic regression (LR) and decision tree learning. Logistic model trees are based on the earlier idea of a model tree: a decision tree that has linear regression models at its leaves to provide a piecewise linear regression model (where ordinary decision trees with constants at their leaves would produce a piecewise constant model).109FDEF6, 292464Minimum message lengthMinimum message length (MML) is a formal information theory restatement of Occam's Razor: even when models are not equal in goodness of fit accuracy to the observed data, the one generating the shortest overall message is more likely to be correct (where the message consists of a statement of the model, followed by a statement of data encoded concisely using that model). MML was invented by Chris Wallace, first appearing in the seminal (Wallace and Boulton, 1968).109FDEF6, 292465Lazy learningIn artificial intelligence, lazy learning is a learning method in which generalization beyond the training data is delayed until a query is made to the system, as opposed to in eager learning, where the system tries to generalize the training data before receiving queries.109FDEF6, 292466Instance-based learninginstance-based learning or memory-based learning is a family of learning algorithms that, instead of performing explicit generalization, compare new problem instances with instances seen in training, which have been stored in memory. Instance-based learning is a kind of lazy learning.109FDEF6, 292475k-nearest neighbor algorithmIn pattern recognition, the k-nearest neighbor algorithm (k-NN) is a non-parametric method for classifying objects based on closest training examples in the feature space. k-NN is a type of instance-based learning, or lazy learning where the function is only approximated locally and all computation is deferred until classification. 109FDEF6, 292478Probably approximately correct learningIn this framework, the learner receives samples and must select a generalization function (called the hypothesis) from a certain class of possible functions. The goal is that, with high probability (the "probably" part), the selected function will have low generalization error (the "approximately correct" part). The learner must be able to learn the concept given any arbitrary approximation ratio, probability of success, or distribution of the samples.109FDEF6, 292480Ripple-down rulesRipple Down Rules is a way of approaching knowledge acquisition. Knowledge acquisition refers to the transfer of knowledge from human experts to knowledge based systems.109FDEF6, 292481Support vector machinesIn machine learning, support vector machines (SVMs, also support vector networks[1]) are supervised learning models with associated learning algorithms that analyze data and recognize patterns, used for classification and regression analysis. 109FDEF6 URL: |
|
|