Details view: Fishers linear discriminant

Fisher's linear discriminant Component1 #302702 Linear discriminant analysis (LDA) and the related Fisher's linear discriminant are methods used in statistics, pattern recognition and machine learning to find a linear combination of features which characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later classification.
Fisher's linear discriminant[edit] The terms Fisher's linear discriminant and LDA are often used interchangeably, although Fisher's original article^[1] actually describes a slightly different discriminant, which does not make some of the assumptions of LDA such as normally distributed classes or equal class covariances. 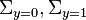Suppose two classes of observations have means $\vec \mu_{y=0}, \vec \mu_{y=1}$ and covariances $\Sigma_{y=0},\Sigma_{y=1}$ . Then the linear combination of features 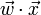$\vec w \cdot \vec x$ will have means 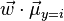$\vec w \cdot \vec \mu_{y=i}$ and variances $\vec w^T \Sigma_{y=i} \vec w$ for $i=0,1$ . 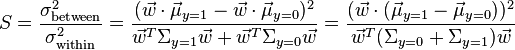Fisher defined the separation between these two distributions to be the ratio of the variance between the classes to the variance within the classes: $S=\frac{\sigma_{\text{between}}^2}{\sigma_{\text{within}}^2}= \frac{(\vec w \cdot \vec \mu_{y=1} - \vec w \cdot \vec \mu_{y=0})^2}{\vec w^T \Sigma_{y=1} \vec w + \vec w^T \Sigma_{y=0} \vec w} = \frac{(\vec w \cdot (\vec \mu_{y=1} - \vec \mu_{y=0}))^2}{\vec w^T (\Sigma_{y=0}+\Sigma_{y=1}) \vec w}$ This measure is, in some sense, a measure of the signal-to-noise ratio for the class labelling. It can be shown that the maximum separation occurs when $\vec w \propto (\Sigma_{y=0}+\Sigma_{y=1})^{-1}(\vec \mu_{y=1} - \vec \mu_{y=0})$ When the assumptions of LDA are satisfied, the above equation is equivalent to LDA. Be sure to note that the vector $\vec w$ is the normal to the discriminant hyperplane. As an example, in a two dimensional problem, the line that best divides the two groups is perpendicular to $\vec w$ . Generally, the data points to be discriminated are projected onto $\vec w$ ; then the threshold that best separates the data is chosen from analysis of the one-dimensional distribution. There is no general rule for the threshold. However, if projections of points from both classes exhibit approximately the same distributions, a good choice would be the hyperplane between projections of the two means, $\vec w \cdot \vec \mu_{y=0}$ and $\vec w \cdot \vec \mu_{y=1}$ . In this case the parameter c in threshold condition $\vec w \cdot \vec x > c$ can be found explicitly: $c = \vec w \cdot \frac12 (\vec \mu_{y=0} + \vec \mu_{y=1}) = \frac{1}{2} \vec\mu_{y=1}^t \Sigma^{-1} \vec\mu_{y=1} - \frac{1}{2} \vec\mu_{y=0}^t \Sigma^{-1} \vec\mu_{y=0}$ .