|
![]()
| Minimum message length Component1 #292464 Minimum message length (MML) is a formal information theory restatement of Occam's Razor: even when models are not equal in goodness of fit accuracy to the observed data, the one generating the shortest overall message is more likely to be correct (where the message consists of a statement of the model, followed by a statement of data encoded concisely using that model). MML was invented by Chris Wallace, first appearing in the seminal (Wallace and Boulton, 1968). | Minimum message length (MML) is a formal information theory restatement of Occam's Razor: even when models are not equal in goodness of fit accuracy to the observed data, the one generating the shortest overall message is more likely to be correct (where the message consists of a statement of the model, followed by a statement of data encoded concisely using that model). MML was invented by Chris Wallace, first appearing in the seminal (Wallace and Boulton, 1968). MML is intended not just as a theoretical construct, but as a technique that may be deployed in practice. It differs from the related concept of Kolmogorov complexity in that it does not require use of a Turing-complete language to model data. The relation between Strict MML (SMML) and Kolmogorov complexity is outlined in Wallace and Dowe (1999a). Further, a variety of mathematical approximations to "Strict" MML can be used — see, e.g., Chapters 4 and 5 of Wallace (posthumous) 2005. Contents [hide] - 1 Definition
- 2 Continuous-valued parameters
- 3 Key features of MML
- 4 See also
- 5 External links
Definition[edit]Shannon's A Mathematical Theory of Communication (1949) states that in an optimal code, the message length (in binary) of an event 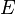 , ,  , where , where 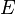 has probability has probability  , is given by , is given by 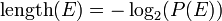 . . Bayes's theorem states that the probability of a (variable) hypothesis 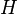 given fixed evidence given fixed evidence 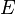 is proportional to is proportional to  , which, by the definition of conditional probability, is equal to , which, by the definition of conditional probability, is equal to  . We want the model (hypothesis) with the highest such posterior probability. Suppose we encode a message which represents (describes) both model and data jointly. Since . We want the model (hypothesis) with the highest such posterior probability. Suppose we encode a message which represents (describes) both model and data jointly. Since  , the most probable model will have the shortest such message. The message breaks into two parts: , the most probable model will have the shortest such message. The message breaks into two parts:  . The first part encodes the model itself. The second part contains information (e.g., values of parameters, or initial conditions, etc.) that, when processed by the model, outputs the observed data. . The first part encodes the model itself. The second part contains information (e.g., values of parameters, or initial conditions, etc.) that, when processed by the model, outputs the observed data. MML naturally and precisely trades model complexity for goodness of fit. A more complicated model takes longer to state (longer first part) but probably fits the data better (shorter second part). So, an MML metric won't choose a complicated model unless that model pays for itself. Continuous-valued parameters[edit]One reason why a model might be longer would be simply because its various parameters are stated to greater precision, thus requiring transmission of more digits. Much of the power of MML derives from its handling of how accurately to state parameters in a model, and a variety of approximations that make this feasible in practice. This allows it to usefully compare, say, a model with many parameters imprecisely stated against a model with fewer parameters more accurately stated. Key features of MML[edit] - MML can be used to compare models of different structure. For example, its earliest application was in finding mixture models with the optimal number of classes. Adding extra classes to a mixture model will always allow the data to be fitted to greater accuracy, but according to MML this must be weighed against the extra bits required to encode the parameters defining those classes.
- MML is a method of Bayesian model comparison. It gives every model a score.
- MML is scale-invariant and statistically invariant. Unlike many Bayesian selection methods, MML doesn't care if you change from measuring length to volume or from Cartesian co-ordinates to polar co-ordinates.
- MML is statistically consistent. For problems like the Neyman-Scott (1948) problem or factor analysis where the amount of data per parameter is bounded above, MML can estimate all parameters with statistical consistency.
- MML accounts for the precision of measurement. It uses the Fisher information (in the Wallace-Freeman 1987 approximation, or other hyper-volumes in other approximations) to optimally discretize continuous parameters. Therefore the posterior is always a probability, not a probability density.
- MML has been in use since 1968. MML coding schemes have been developed for several distributions, and many kinds of machine learners including unsupervised classification, decision trees and graphs, DNA sequences, Bayesian networks, neural networks (one-layer only so far), image compression, image and function segmentation, etc.
See also[edit]External links[edit] - Links to all Chris Wallace's known publications.
- C.S. Wallace, Statistical and Inductive Inference by Minimum Message Length, Springer-Verlag (Information Science and Statistics), ISBN 0-387-23795-X, May 2005 - chapter headings, table of contents and sample pages.
- A searchable database of Chris Wallace's publications.
- Minimum Message Length and Kolmogorov Complexity (by C.S. Wallace and D.L. Dowe, Computer Journal, Vol. 42, No. 4, 1999, pp270-283).
- History of MML, CSW's last talk.
- Message Length as an Effective Ockham's Razor in Decision Tree Induction, by S. Needham and D. Dowe, Proc. 8th International Workshop on AI and Statistics (2001),pp253-260. (Shows how Occam's razor works fine when interpreted as MML.)
- L.Allison,
Models for machine learning and data mining in functional programming, J. Functional Programming, 15(1), pp15-32, Jan. 2005 (MML, FP, and Haskell code). [See also Comley and Dowe (2003), .pdf. Comley & Dowe (2003, 2005) are the first two papers on MML Bayesian nets using both discrete and continuous valued parameters.] - Dowe, David L. (2010). MML, hybrid Bayesian network graphical models, statistical consistency, invariance and uniqueness, in Handbook of Philosophy of Science (Volume 7: Handbook of Philosophy of Statistics), Elsevier, ISBN 978-0-444-51862-0, pp901-982.
- Minimum Message Length (MML), LA's MML introduction, (MML alt.).
- Minimum Message Length (MML), researchers and links.
- Another MML research website.
- Snob page for MML mixture modelling.
- MITECS: Chris Wallace wrote an entry on MML for MITECS. (Requires account)
- mikko.ps: Short introductory slides by Mikko Koivisto in Helsinki]
- Akaike information criterion (AIC) method of model selection, and a comparison with MML: D.L. Dowe, S. Gardner & G. Oppy (2007), "Bayes not Bust! Why Simplicity is no Problem for Bayesians", Brit. J. Philos. Sci., Vol. 58, Dec. 2007, pp709-754.
|
+Citations (1) - CitationsAdd new citationList by: CiterankMapLink[1] Wikipedia
Author: Various
Cited by: Roger Yau 2:08 PM 21 October 2013 GMT
Citerank: (28) 291862AODE - Averaged one-dependence estimatorsAveraged one-dependence estimators (AODE) is a probabilistic classification learning technique. It was developed to address the attribute-independence problem of the popular naive Bayes classifier. It frequently develops substantially more accurate classifiers than naive Bayes at the cost of a modest increase in the amount of computation.109FDEF6, 291863Artificial neural networkIn computer science and related fields, artificial neural networks are computational models inspired by animal central nervous systems (in particular the brain) that are capable of machine learning and pattern recognition. They are usually presented as systems of interconnected "neurons" that can compute values from inputs by feeding information through the network.109FDEF6, 291936BackpropagationBackpropagation, an abbreviation for "backward propagation of errors", is a common method of training artificial neural networks. From a desired output, the network learns from many inputs, similar to the way a child learns to identify a dog from examples of dogs.109FDEF6, 291937Bayesian statisticsBayesian statistics is a subset of the field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities. Such an interpretation is only one of a number of interpretations of probability and there are other statistical techniques that are not based on "degrees of belief".109FDEF6, 291938Naive Bayes classifierA naive Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem with strong (naive) independence assumptions. A more descriptive term for the underlying probability model would be "independent feature model". An overview of statistical classifiers is given in the article on Pattern recognition.109FDEF6, 291939Bayesian networkA Bayesian network, Bayes network, belief network, Bayes(ian) model or probabilistic directed acyclic graphical model is a probabilistic graphical model (a type of statistical model) that represents a set of random variables and their conditional dependencies via a directed acyclic graph (DAG). For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. 109FDEF6, 291941Case-based reasoningCase-based reasoning (CBR), broadly construed, is the process of solving new problems based on the solutions of similar past problems. An auto mechanic who fixes an engine by recalling another car that exhibited similar symptoms is using case-based reasoning. So, too, an engineer copying working elements of nature (practicing biomimicry), is treating nature as a database of solutions to problems. Case-based reasoning is a prominent kind of analogy making.109FDEF6, 291942Decision tree learningDecision tree learning uses a decision tree as a predictive model which maps observations about an item to conclusions about the item's target value. It is one of the predictive modelling approaches used in statistics, data mining and machine learning. More descriptive names for such tree models are classification trees or regression trees. In these tree structures, leaves represent class labels and branches represent conjunctions of features that lead to those class labels.109FDEF6, 291943Inductive logic programmingInductive logic programming (ILP) is a subfield of machine learning which uses logic programming as a uniform representation for examples, background knowledge and hypotheses. Given an encoding of the known background knowledge and a set of examples represented as a logical database of facts, an ILP system will derive a hypothesised logic program which entails all the positive and none of the negative examples.109FDEF6, 291944Gaussian process regression (Kriging)Kriging is a method to build an approximation of a function from a set of evaluations of the function at a finite set of points. The method originates from the domain of geostatistics and is now widely used in the domain of spatial analysis and computer experiments. The technique is also known as Gaussian process regression, Kolmogorov Wiener prediction, or Best Linear Unbiased Prediction.109FDEF6, 291945Gene expression programmingGene expression programming (GEP) is an evolutionary algorithm that creates computer programs or models. These computer programs are complex tree structures that learn and adapt by changing their sizes, shapes, and composition, much like a living organism. And like living organisms, the computer programs of GEP are also encoded in simple linear chromosomes of fixed length. Thus, GEP is a genotype-phenotype system.109FDEF6, 291946Group method of data handlingGroup method of data handling (GMDH) is a family of inductive algorithms for computer-based mathematical modeling of multi-parametric datasets that features fully automatic structural and parametric optimization of models.109FDEF6, 291947Learning automataA branch of the theory of adaptive control is devoted to learning automata surveyed by Narendra and Thathachar which were originally described explicitly as finite state automata. Learning automata select their current action based on past experiences from the environment.109FDEF6, 291948Supervised learningSupervised learning is the machine learning task of inferring a function from labeled training data.[1] The training data consist of a set of training examples. In supervised learning, each example is a pair consisting of an input object (typically a vector) and a desired output value (also called the supervisory signal). A supervised learning algorithm analyzes the training data and produces an inferred function, which can be used for mapping new examples. 25CBCBFF, 291950Unsupervised learningIn machine learning, the problem of unsupervised learning is that of trying to find hidden structure in unlabeled data. Since the examples given to the learner are unlabeled, there is no error or reward signal to evaluate a potential solution. This distinguishes unsupervised learning from supervised learning and reinforcement learning.25CBCBFF, 291951Reinforcement learningReinforcement learning is an area of machine learning inspired by behaviorist psychology, concerned with how software agents ought to take actions in an environment so as to maximize some notion of cumulative reward. The problem, due to its generality, is studied in many other disciplines, such as game theory, control theory, operations research, information theory, simulation-based optimization, statistics, and genetic algorithms.25CBCBFF, 292450Hierarchical clusteringIn data mining, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:
Agglomerative: This is a "bottom up" approach: each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy.
Divisive: This is a "top down" approach: all observations start in one cluster, and splits are performed recursively as one moves down the hierarch109FDEF6, 292451Association rule learningAssociation rule learning is a popular and well researched method for discovering interesting relations between variables in large databases. It is intended to identify strong rules discovered in databases using different measures of interestingness.109FDEF6, 292454Others25CBCBFF, 292455Learning Vector QuantizationIn computer science, Learning Vector Quantization (LVQ), is a prototype-based supervised classification algorithm. LVQ is the supervised counterpart of vector quantization systems.
LVQ can be understood as a special case of an artificial neural network, more precisely, it applies a winner-take-all Hebbian learning-based approach. It is a precursor to Self-organizing maps (SOM) and related to Neural gas, and to the k-Nearest Neighbor algorithm (k-NN). LVQ was invented by Teuvo Kohonen.109FDEF6, 292463Logistic Model TreeLMT is a classification model with an associated supervised training algorithm that combines logistic regression (LR) and decision tree learning. Logistic model trees are based on the earlier idea of a model tree: a decision tree that has linear regression models at its leaves to provide a piecewise linear regression model (where ordinary decision trees with constants at their leaves would produce a piecewise constant model).109FDEF6, 292465Lazy learningIn artificial intelligence, lazy learning is a learning method in which generalization beyond the training data is delayed until a query is made to the system, as opposed to in eager learning, where the system tries to generalize the training data before receiving queries.109FDEF6, 292466Instance-based learninginstance-based learning or memory-based learning is a family of learning algorithms that, instead of performing explicit generalization, compare new problem instances with instances seen in training, which have been stored in memory. Instance-based learning is a kind of lazy learning.109FDEF6, 292475k-nearest neighbor algorithmIn pattern recognition, the k-nearest neighbor algorithm (k-NN) is a non-parametric method for classifying objects based on closest training examples in the feature space. k-NN is a type of instance-based learning, or lazy learning where the function is only approximated locally and all computation is deferred until classification. 109FDEF6, 292476Analogical modelingAnalogical modeling (hereafter AM) is a formal theory of exemplar-based analogical reasoning, proposed by Royal Skousen, professor of Linguistics and English language at Brigham Young University in Provo, Utah. It is applicable to language modeling and other categorization tasks. Analogical modeling is related to connectionism and nearest neighbor approaches, in that it is data-based rather than abstraction-based.109FDEF6, 292478Probably approximately correct learningIn this framework, the learner receives samples and must select a generalization function (called the hypothesis) from a certain class of possible functions. The goal is that, with high probability (the "probably" part), the selected function will have low generalization error (the "approximately correct" part). The learner must be able to learn the concept given any arbitrary approximation ratio, probability of success, or distribution of the samples.109FDEF6, 292480Ripple-down rulesRipple Down Rules is a way of approaching knowledge acquisition. Knowledge acquisition refers to the transfer of knowledge from human experts to knowledge based systems.109FDEF6, 292481Support vector machinesIn machine learning, support vector machines (SVMs, also support vector networks[1]) are supervised learning models with associated learning algorithms that analyze data and recognize patterns, used for classification and regression analysis. 109FDEF6 URL: |
|
|