A full-sized version of the original can be ordered here.

• Are connectionist networks like human neural networks?
• Do connectionist networks follow rules?
• Are connectionist networks vulnerable to the arguments against physical symbol systems?
• Does the subsymbolic paradigm offer a valid account of connectionism?
• Can connectionist networks exhibit systematicity?
• Other connectionist arguments

• an ability to learn via training rather than explicit programming
• parallel and distributed processing
• neural realism, or at least neural inspiration
• fluid tolerance of noisy or incomplete data
• superior performance on perceptual and motor tasks

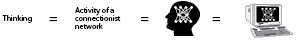
Note: This general characterization of connectionism is intended to highlight those aspects of the field that there are relevant to this map. Few connectionist would actually claim that 'connectionist networks can think', because connectionist networks are usually regarded as simulations of neural networks in the brain, which is where the real thinking is understood to take place.

Postulates of Connectionism

1) There is a set of elements called units or notes.

2) Nodes pass signals (numerical values) to each other.

3) Nodes are connected into networks which resemble neural networks in the brain.

4) When a set of signals reaches a node, they are multiplied by weights and then are added together to produce an activation value.

5) The activation value is then passed to an output function, which decides what final value a unit should output.

6) Vectors (sets of numeric values) are the basic representational medium of a connectionist network. Vectors enter the network as input, are processed to vectors (and matrices) of weights and connections, and new vectors are produced as a result.

7) Neural networks are trained to compute vector-to-vector functions. That is, they learn to convert specific input vectors to specific output vectors.

8) Learning takes place at the weights, which are adjusted using a variety of learning procedures, generally involving exposure to a corpus of sample inputs.

Proponents include: David Rumelhart, Paul Smolensky, James McClelland, Geoff Hinton, Jerry Feldman, Paul and Patricia Churchland, Terrence Horgan, John Tienson, David Tourestsky, Jeff Ellman, Stephen Grossberg, & Terrence Sejnowski.

Learning in Connectionist Networks

Connectionist networks learn by incrementally adjusting their weights in response to a corpus of sampling points. The networks are repeatedly fed these inputs until they have been trained to perform as desired. Training takes place via learning algorithm.

Learning is a central emphasis in connectionism, and there is a vast technical literature on the various connectionist learning algorithms. The most widespread learning procedure is the backpropagation algorithm, which changes the weights of the feed-forward network based on the error generated by a given input. Other important learning algorithms include: competitive learning and the Boltzmann machine learning algorithm.

History of Connectionism

Several historical precursors to connectionism are cited in the literature. It is sometimes claimed that Aristotle, with his focus on learning and intuition, was a proto-connectionist. The works of the British Empiricists (John Locke, George Berkeley, and David Hume) are also viewed as precursors to connectionism, given that associative links between ideas are similar to weighted links between nodes. (Note that the Empiricists are also pinpointed as precursors to classical AI.

Formal analysis of neural networks was pioneered by biologists and cyberneticists in the 1940s & 1950s. Warren McCulloch & Warrren Pitts (1943) developed a logical calculus of neural activity, which showed that neuron-like elements could compute logical functions.

Donald Hebb (1949) proposed that learning in neural networks takes place when two connected units are simultaneously active. Frank Rosenblatt (1959) may have been the first modern connectionist. His perceptron’ (one-layer feedforward networks) could learn to recognise patterns reasonably well, and he develops early forms of several modern learning schemes. Rosenblatt also introduced the use of computer simulation into neural networks theory.

From the late 1950s to the 1970s there was a lull in connectionist research, which resulted from the early success of AI combined with Marvin Minsky's & Seymour Papert's critique of perceptrons, which was developed throughout the 1960s (but not published until 1969). Their critique showed that one-layer networks couldn't compute certain kinds of functions.

Connectionism began to resurface in the 1970s. One of the classic papers of the new generation was Jerome Feldman and Dana Ballard’s Connectionist models and their properties (1982), which introduced the term connectionism, outlined some of the basic properties of connectionist models, and argued for their superiority over classical AI systems. The major publication of this new generation was David Rumelhart, James McClelland, and the PDP research group's Parallel Distributed Processing volumes (1986), which sold out upon publication and which rallied many AI researchers to the connectionist camp. The writers describe modern connectionist research in detail and argued tfor he superiority of connectionism over classical symbolic AI.

Renewed interest in connectionism was answered by the classical AI camp with a series of polemics, in particular a special issue of Cognition (1988), which contained three long critiques of connectionism by prominent cognitive scientists. The gist of three Cognition arguments is the same: 1) connectionism is a revival of associationist series, which are cognitively weak; 2) such theories can’t account for the kind of systematicity generatiiity that symbolic accounts explain so well; and, 3) if connectionism can account for such phenomena, it offers a mere implementation of the classical view.

The debate between connectionists & classicists, which has been called a "holy war" and "a battle to win souls", continues. Although the debate has often been heated, current discussions lean increasingly towards ecumenical views, which try to give credit to the virtues of both classical and connectionist approaches.

Further history is contained in Rumelhart & McClelland (1986b, pp.41-44), and in Russell & Norvig (1985, pp.594-596).