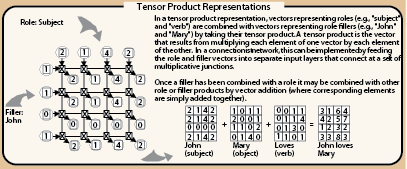
Tensor product representations
Tensor product representations have constituent structure but are distributed and context sensitive in a nonclassical way; thereby, avoiding the dilemma (see detailed text).
Vectors representing
roles (e.g. subject or object) and
fillers (e.g. John, Mary, loves, etc) can be bound together by a network that takes the tensor product of the two vectors. The vectors that result are then added together to produce complex representations.
Paul Smolensky (1988a).
Tensor Product RepresentationsIn a tensor product representation, vectors representing
roles (e.g. subject and verb) are combined with vectors representing role
fillers (e.g. John and Mary) by taking their
tensor product.
A
tensor product is the vector that results from multiplying each element of one vector by each element of the other.
In a connectionist network, this can be implemented by feeding the role and filler vectors into separate input layers that connect at a set of multiplicative joints.
Once a filler has been combined with a role it may be combined with other role or filler products by vector addition (with corresponding elements are simply added together).