comments

FastICA

FastICA is an efficient and popular algorithm for independent component analysis invented by Aapo Hyvärinen at Helsinki University of Technology. The algorithm is based on a fixed-point iteration scheme maximizing non-Gaussianity as a measure of statistical independence. It can also be derived as an approximative Newton iteration.

FastICA is an efficient and popular algorithm for independent component analysis invented by Aapo Hyvärinen at Helsinki University of Technology. The algorithm is based on a fixed-point iteration scheme maximizing non-Gaussianity as a measure ofstatistical independence. It can also be derived as an approximative Newton iteration.

 

Contents

  [hide] 
  • 1 Algorithm
    • 1.1 Preprocess the data
      • 1.1.1 Centering the data
      • 1.1.2 Whitening the data
    • 1.2 Single component extraction
    • 1.3 Multiple component extraction
  • 2 See also
  • 3 References
  • 4 External links

 

Algorithm[edit]

Preprocess the data[edit]

Before the FastICA algorithm can be applied, the input vector data \mathbf{x} should be centered and whitened.

Centering the data[edit]

The input data \mathbf{x} is centered by computing the mean of each component of \mathbf{x} and subtracting that mean. This has the effect of making each component have zero mean. Thus:

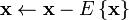
\mathbf{x} \leftarrow \mathbf{x} - E\left\{\mathbf{x}\right\}

Whitening the data[edit]

Whitening the data involves linearly transforming the data so that the new components are uncorrelated and have variance one. If 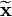\widetilde{\mathbf{x}} is the whitened data, then the covariance matrix of the whitened data is the identity matrix:

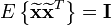
E\left \{ \widetilde{\mathbf{x}} \widetilde{\mathbf{x}}^{T} \right \} = \mathbf{I}

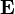This can be done using eigenvalue decomposition of the covariance matrix of the data:  E\left \{ \mathbf{x} \mathbf{x}^{T} \right \} = \mathbf{E}\mathbf{D}\mathbf{E}^T, where \mathbf{E} is the matrix of eigenvectors and \mathbf{D} is the diagonal matrix of eigenvalues. Once eigenvalue decomposition is done, the whitened data is:

\mathbf{x} \leftarrow \mathbf{E}\mathbf{D}^{-1/2}\mathbf{E}^T\mathbf{x}

Single component extraction[edit]

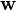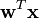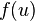The iterative algorithm finds the direction for the weight vector \mathbf{w} maximizing the non-Gaussianity of the projection \mathbf{w}^T \mathbf{x} for the data \mathbf{x}. The function g(u) is the derivative of a nonquadratic nonlinearity function f(u). Hyvärinen states that good equations for f (shown with their derivatives g and second derivatives {g}') are:

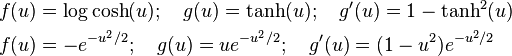
\begin{align}f(u) &= \log \cosh (u); \quad g(u) = \tanh (u); \quad {g}'(u) = 1-\tanh^2(u) \\f(u) &= -e^{-u^2/2}; \quad g(u) = u e^{-u^2/2}; \quad {g}'(u) = (1-u^2) e^{-u^2/2}\end{align}

The first equation is a good general-purpose equation, while the second is highly robust.

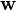
  1. Randomize the initial weight vector \mathbf{w}
  2. Let 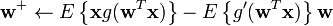 \mathbf{w}^+ \leftarrow E\left\{\mathbf{x} g(\mathbf{w}^T \mathbf{x})\right\} - E\left\{g'(\mathbf{w}^T \mathbf{x})\right\}\mathbf{w} , where 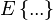E\left\{...\right\} means averaging over all column-vectors of matrix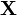 \mathbf{X}
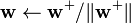
  3. Let  \mathbf{w} \leftarrow \mathbf{w}^+ / \|\mathbf{w}^+\|
  4. If not converged, go back to 2

Multiple component extraction[edit]

The single unit iterative algorithm only estimates one of the independent components, to estimate more the algorithm must repeated, and the projection vectors decorated. Although Hyvärinen provides several ways of decorating results the simplest multiple unit algorithm follows. \mathbf{1} indicates a column vector of 1's with dimension M.

Algorithm FastICA

Input: 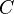 C  Number of desired components
Input:  \mathbf{X} \in \mathbb{R}^{N \times M}  Matrix, where each column represents an N-dimensional sample, where 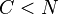 C < N
Output: 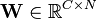 \mathbf{W} \in \mathbb{R}^{C \times N}  Un-mixing matrix where each row projects X onto into independent component.
Output:  \mathbf{S} \in \mathbb{R}^{C \times M}  Independent components matrix, with M columns representing a sample with C dimensions.
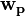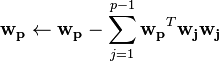
for p in 1 to C:    \mathbf{w_p} \leftarrow Random vector of length N    while \mathbf{w_p} changes        \mathbf{w_p} \leftarrow \frac{1}{M}\mathbf{X} g(\mathbf{w_p}^T \mathbf{X}) - \frac{1}{M}g'(\mathbf{w_p}^T\mathbf{X})\mathbf{1} \mathbf{w_p}        \mathbf{w_p} \leftarrow \mathbf{w_p} - \sum_{j = 1}^{p-1} \mathbf{w_p}^T\mathbf{w_j}\mathbf{w_j}        \mathbf{w_p} \leftarrow \frac{\mathbf{w_p}}{\|\mathbf{w_p}\|}Output:  \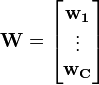mathbf{W} = \begin{bmatrix} \mathbf{w_1} \\ \vdots \\ \mathbf{w_C} \end{bmatrix}Output:  \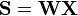mathbf{S} = \mathbf{W}\mathbf{X}

See also[edit]

References[edit]

External links[edit]

RELATED ARTICLESExplain
⌅
Machine Learning Methods & Algorithms
⌃
Unsupervised learning
■
FastICA
□
Association rule learning
□
Data clustering
□
Expectation–maximization algorithm
□
Generative topographic map
□
Hierarchical clustering
□
IBSEAD - distributed autonomous entity systems based Interaction
□
Information bottleneck method
□
Partitional clustering
□
Radial basis function network
□
Self-organizing map
□
Sparse PCA (sparse principal component analysis)
□
Stochastic gradient descent
□
Vector quantization (VQ)
□
Graph of this discussion
Enter the title of your article


Enter a short (max 500 characters) summation of your article
Enter the main body of your article
Lock
+Comments (0)
+Citations (0)
+About
Enter comment

Select article text to quote
welcome text

First name   Last name 

Email

Skip