comments

Probably approximately correct learning

In this framework, the learner receives samples and must select a generalization function (called the hypothesis) from a certain class of possible functions. The goal is that, with high probability (the "probably" part), the selected function will have low generalization error (the "approximately correct" part). The learner must be able to learn the concept given any arbitrary approximation ratio, probability of success, or distribution of the samples.

In computational learning theory, probably approximately correct learning (PAC learning) is a framework for mathematical analysis of machine learning. It was proposed in 1984 byLeslie Valiant.[1]

In this framework, the learner receives samples and must select a generalization function (called the hypothesis) from a certain class of possible functions. The goal is that, with high probability (the "probably" part), the selected function will have low generalization error (the "approximately correct" part). The learner must be able to learn the concept given any arbitrary approximation ratio, probability of success, or distribution of the samples.

The model was later extended to treat noise (misclassified samples).

An important innovation of the PAC framework is the introduction of computational complexity theory concepts to machine learning. In particular, the learner is expected to find efficient functions (time and space requirements bounded to a polynomial of the example size), and the learner itself must implement an efficient procedure (requiring an example count bounded to a polynomial of the concept size, modified by the approximation and likelihood bounds).

Contents

  [hide] 
  • 1 Definitions and terminology
  • 2 Equivalence
  • 3 References
  • 4 Further reading

Definitions and terminology[edit]

In order to give the definition for something that is PAC-learnable, we first have to introduce some terminology.[2] [3]

For the following definitions, two examples will be used. The first is the problem of character recognition given an array of n bits. The other example is the problem of finding an interval that will correctly classify points within the interval as positive and the points outside of the range as negative.

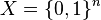Let X be a set called the instance space or the encoding of all the samples, and each instance have length assigned. In the character recognition problem, the instance space is X=\{0,1\}^n. In the interval problem the instance space is 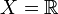X=\mathbb{R}, where \mathbb{R} denotes the set of all real numbers.

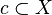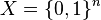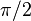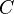A concept is a subset c \subset X. One concept is the set of all patterns of bits in X=\{0,1\}^n that encode a picture of the letter "P". An example concept from the second example is the set of all of the numbers between \pi/2 and \sqrt{10}. A concept class C is a set of concepts over X. This could be the set of all subsets of the array of bits that are skeletonized 4-connected (width of the font is 1).

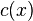Let EX(c,D) be a procedure that draws an example, x, using a probability distribution D and gives the correct label c(x), that is 1 if 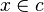x \in c and 0 otherwise.

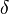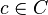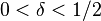Say that there is an algorithm A that given access to EX(c,D) and inputs \epsilon and \delta that, with probability of at least 1-\delta, A outputs a hypothesis h \in C that has error less than or equal to \epsilon with examples drawn from X with the distribution D. 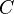If there is such an algorithm for every concept c \in C, for every distribution D over X, and for all 0<\epsilon<1/2 and 0<\delta<1/2 then C is PAC learnable (or distribution-free PAC learnable). We can also say that A is a PAC learning algorithm for C.

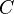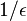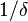An algorithm runs in time t if it draws at most t examples and requires at most t time steps. A concept class is efficiently PAC learnable if it is PAC learnable by an algorithm that runs in time polynomial in 1/\epsilon, 1/\delta and instance length.

Equivalence[edit]

Under some regularity conditions these three conditions are equivalent:

  1. The concept class C is PAC learnable.
  2. The VC dimension of C is finite.
  3. C is a uniform Glivenko-Cantelli class.

References[edit]

  1. Jump up^ L. Valiant. A theory of the learnable. Communications of the ACM, 27, 1984.
  2. Jump up^ Kearns and Vazirani, pg. 1-12,
  3. Jump up^ Balas Kausik Natarajan, Machine Learning , A Theoretical Approach, Morgan Kaufmann Publishers, 1991

Further reading[edit]

RELATED ARTICLESExplain
⌅
Machine Learning Methods & Algorithms
⌃
Supervised learning
■
Probably approximately correct learning
□
AODE - Averaged one-dependence estimators
□
Artificial neural network
□
Bayesian statistics
□
Case-based reasoning
□
Conditional Random Field
□
Decision tree learning
□
Ensemble learning
□
Gaussian process regression (Kriging)
□
Gene expression programming
□
Group method of data handling
□
Inductive logic programming
□
Information Fuzzy Networks (IFN)
□
Instance-based learning
□
Large-Scale Supervised Sparse Principal Component Analysis
□
Lazy learning
□
Learning automata
□
Learning Vector Quantization
□
Logistic Model Tree
□
Minimum message length
□
Minimum redundancy feature selection
□
Ordinal classification
□
Random Forests
□
Regression analysis
□
Ripple-down rules
□
Statistical classification
□
Subsymbolic machine learning
□
Support vector machines
□
Symbolic machine learning
□
Graph of this discussion
Enter the title of your article


Enter a short (max 500 characters) summation of your article
Enter the main body of your article
Lock
+Comments (0)
+Citations (1)
+About
Enter comment

Select article text to quote
welcome text

First name   Last name 

Email

Skip