November 25, 2014 at 4:46 pm comment to Quanta
For a broader discussion of the "dual paradigm view" (interpreting mathematical systems theory from direct study of individual systems), see the brief article responding to David Pines article for SFRI saying that for systems science to progress now, it needs a way to study actual complex systems. This is comment seems to be more engaging than my first response that didn't get published.
It’s interesting that with such a number of cross connecting areas of physics being discussed, the ultimate finding technically didn't answer the initial question posed. That was Robert May’s “question about whether a complex ecosystem can ever be stable, or whether interactions between species inevitably lead some to wipe out others”.
The mathematical analysis of that question and others was limited to “kinds of random growth” and “systems of correlated random variables”. There are also lots of non-randomly behaving systems too is worth considering, and may have been overlooked in answering the basic question. The variety of organizational growth systems that are familiar everywhere in nature display many kinds of growth curves and outcomes, often having an overall appearance of being 1) quite lopsided, 2) quite symmetric, or 3) reaching extended stable states.
note: How the meaning of probability distribution curve shapes (as discussed in the article) differs from the meaning of these individual development curve shapes was skipped in this short comment on the article. Please do bring it up of course if needed. The question posed was about the development of individual ecosystems, and their potential structural stability.
Generic common curve shapes
for the development of organizational systems.
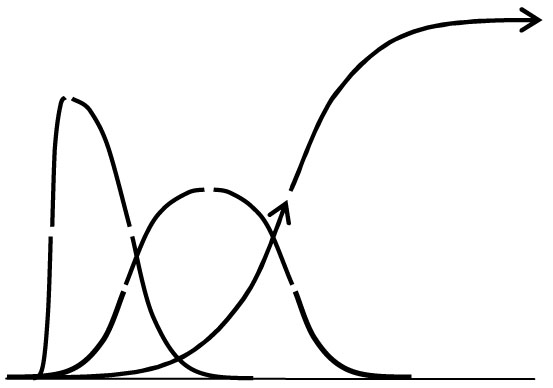
We probably know of lots familiar examples of these from personal experience, where the systems involved are going through progressive organizational change during their periods of acceleration or deceleration. Reversals in curvature don’t always reflect systemic changes in direction for organizational development, but often do though (shown as gaps in the diagram for raising those questions).
The one looking like a TW distribution curve is familiar to all economics and other matters, as a “meteoric rise” followed by “immediate decline”, like many a seemingly fine business plans might experience. The quite unusual thing is this same shape turns up in Gamma Ray burst records too (see image of BATSE 551 #1 below). It raises the question of whether that system (presumably of radiation from black hole collapse) reflects the organizational stages of a system that experiences a “blows out” (like some of our best business plans do) or that of a statistical distribution for correlated variables, or something else?
In any case, just asking that raises the possibility of a bridge between TW correlations and the fates of natural system organization designs, and perhaps a need to consider whether the other kinds of system are available to change the outcome for May’s ecosystems, depending on their design.
Gamma Ray Burst “BATSE 551 #1”
- Raw data dynamically smoothed -
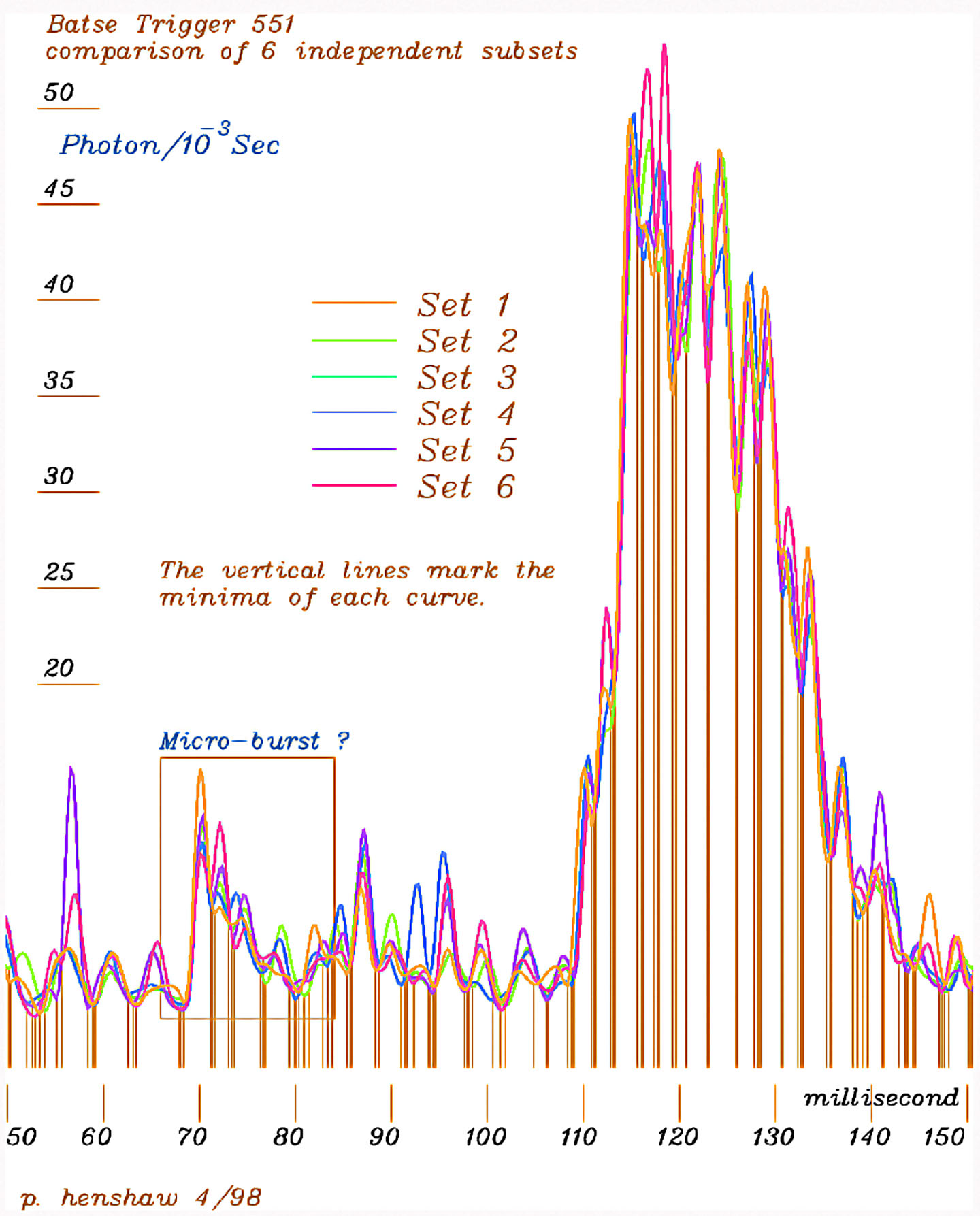
( reposted on the Reading Nature's Signals
________________
jlh